Update
Steve McIntyre has taken exception to this post, with his own post entitled Sliming by Stokes. He has claimed in the comments here that:
"Stokes’ most recent post, entitled “What Steve McIntyre Won’t Show You Now”, contains a series of lies and fantasies, falsely claiming that I’ve been withholding MM05-EE analyses from readers in my recent fisking of ClimateBaller doctrines, falsely claiming that I’ve “said very little about this recon [MM05-EE] since it was published” and speculating that I’ve been concealing these results because they were “inconvenient”."
I've responded in a comment at CA giving chapter and verse on how he avoided telling the Congressional Committe to which he testified, which had a clear interest, about these inconvenient results. So far, no response (and of course no apology for the "sliming").
That was shown in MM05EE, their 2005 Paper titled:
"The M&M critique of the MBH98 Northern Hemisphere climate index: update and implications". I've shown that plot in an appendix here, and I'll show it again below. But for here, I'll show the plot with the MBH decentered and M&M centered superimposed.
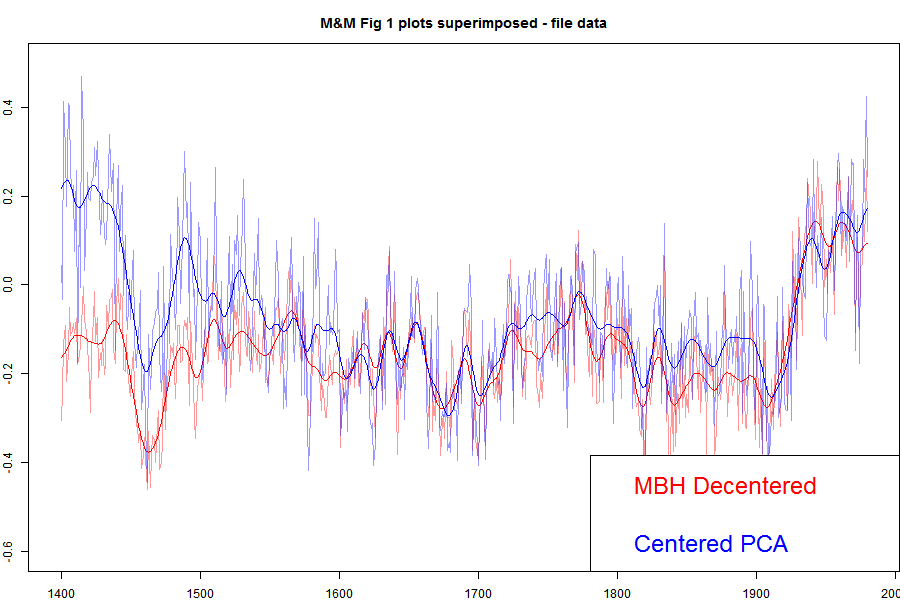
Update: When I printed out the data from my running of the MM05 code for Carrick below, I noticed discrepancies between the numbers and the emulation.txt data on file. I've tried to track down the reason, but I think the simplest thing to do is to switch to using the emulation.txt data directly, which I've done. The MBH and the corrected still track closely in recent centuries, but there is a somewhat larger discrepancy in the 19th century. Prvious versions are here and here..
The agreement is very good between, say, 1800 and 1980. These are the years when all the alleged mined hockey sticks should be showing up. They aren't. There is a discrepancy in the earlier years, which DeepClimate explains here. When Wahl and Ammann corrected various difference between the M&M emulation and MBH99 (in their case) this early period discrepancy disappeared. But anyway, for now what is important is that both centered and uncentered agree very well in the period where decentering is supposed to be mining for hockeysticks. Steve Mc has said very little about this recon since it was published, so much so that when Wegman was pressed (properly) by Rep Stupak at Congress on why he hadn't shown the results of a corrected calculation, he had no good answer, and didn't refer to M&M2005, even though he was supposed to be familiar with the code (which he had) which did it. I think this has become a very inconvenient graph.
I described earlier how apparent PC1 alignments have an effect on reconstruction that disappears rapidly as more than one PC are used. I'll give below a geometric explanation for this, which explains the irrelevance of MM)5 fig 2, which resurfaced as Wegman's fig 4.2.
Here is the plot direct from MM05EE. The bottom "centered" includes the removal by M&M of the Gaspe cedar data from 1400-1450, which affects those years.
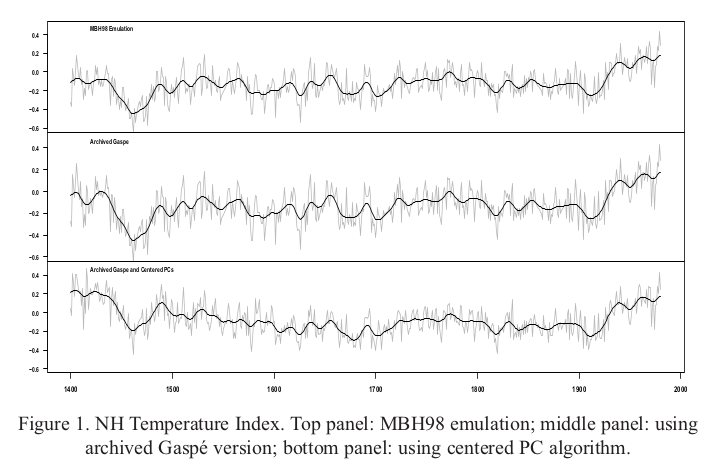
I've described the Gaspe issue, with some more plots here.
With trouble over the 100/1 sampling, Steve McIntyre has promoted his histogram, which appeared as Fig 2 in the MM2005 GRL paper, and as Fig 4.2 in the Wegman Report. The present re-presentation as a t-statistic adds nothing.
I've explained any times how all PCA is doing here is realigning the axes so that PC1 aligns with HS behaviour. In the simulated case, without that the axis directions are not strongly determined, and with white noise, not determined at all. That last means that all possible configurations are equivalent and would give the same results in any analysis. It takes only a slight pertuebation for one alignment to be preferred - how strongly depends on the randomness, not how much difference the alignment makes. I used the following analogy at CA:
Again there is no evidence that any aspect of Mann's decentered PCA has ever affected a temperature reconstruction, despite all the irrelevant graphics about PC1.
"Let me give a geometric analogy here. Suppose you live on a non-rotating spherical earth. You want a coordinate system to calc average temperature, say. You want that system to have a principal axis along the longest radius. You send out teams to measure. Their results have no preferred direction. There is a Pole star, so you histogram a Northness Index. It looks like the first one here. A sort of cos.
Now suppose the Earth is very slightly prolate, N-S, but the limit of measurement. Your teams will return results with a N-S bias. Your histogram of Northness will lbe bimodal like the second above. The spread will depend on how good the measuring is relative to the prolateness. If measurement is good, there will be rare few values, and the two peaks will be sharp.
The definiteness of the histogram has nothing to do with whether alignment of the principal axis matters."
Update. Here is the corresponding emulation from Ammann and Wahl. There is now no large discrepancy in the earleir years.
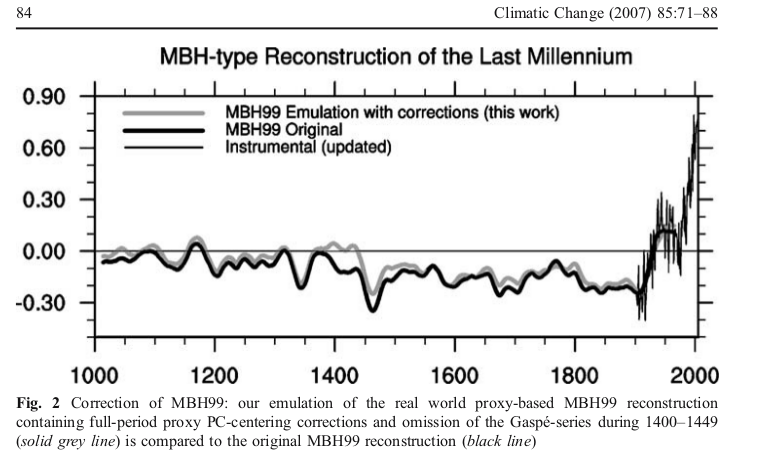
Update: DeepClimate, in a comment here, has linked to the plot below, which shows just how far MM2005 deviated from the MBH recon with centered mean - this time shown against the millenium recon.
Update: Pekka has added a comment which I reproduce with diagram below:
Pekka Pirilä October 8, 2014 at 9:00 AM
As this issue has been discussed so much, I wanted to understand it better and reproduced four variations of PCA of the NORAM1400 network:
1) short-centered MBH98
2) scaling as in MBH98, but fully centered
3) standard scaling and centering
4) without scaling of the original time series (MM05)
Otherwise the results are as reported elsewhere (e.g. in Wahl and Ammann, 2007), but I added the comparison of, how much each PCA explains by up to 10 first PCs calculating the shares from the real variability of time series used in each analysis. Thus the shares are calculated from the same total variance in cases (1) and (2), from slightly different in (3) and from substantively different in (4) where the variances of individual time series vary greatly.
The results are shown here

What many may find surprising is that my numbers for MBH98 are very different from those shown in several places (e.g. RealClimate). The reason is that those numbers are not based on the variability of the time series, but on variances around the short-centered mean. That adds both to the total variance and to the contributions from individual PCs. In relative terms it adds much more to PC1 than to the total. Thus the resulting number does not tell about the real variability, but is very much affected by the decentering.
I calculated my values by first orthonormalizing the basis relative to deviations from full mean (the mean affects, what's orthogonal), and by using this orthonormal basis for determining, how much the space spanned by N first PCs of the MBH98 analysis can explain.