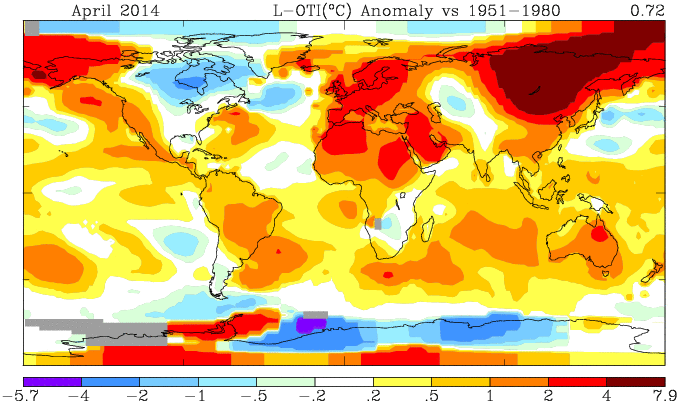
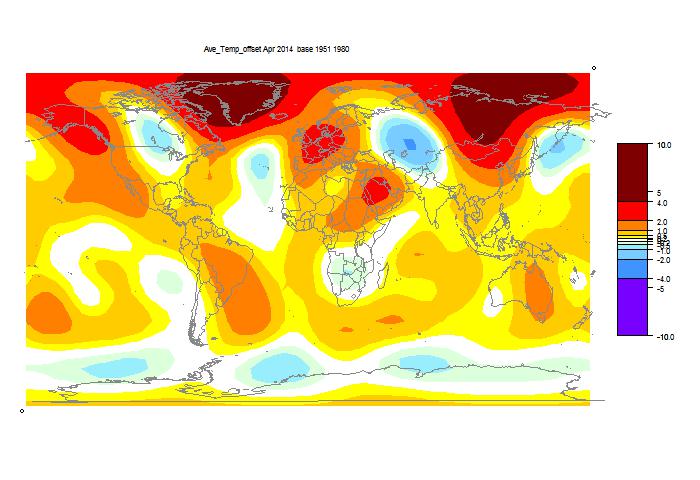
I've been following, and occasionally joining in, a series of threads by Willis Eschenbach at WUWT. Here is the latest, and you can follow links back.
Willis is trying to detect periodicity in various segments (century or so) of monthly or annual data. Lately he has been trying to decide whether sunspot (SSN) periodicities can be observed in climate data. This involves first establishing the major periodicities in SSN, and then looking at periodicities in signals which might be responding.
In the early part, Willis was fitting sinusoids using a least squares fit by optimisation. In this comment, I showed that the quadratic form could be expressed as a fairly orthodox discrete Fourier Transform expression, and wrote code to show how the same result could be derived. Willis then recharacterised what he was doing as a Slow Fourier Transform; here I try to put that in context.
I was not, BTW trying to suggest that what Willis was doing was wrong; only to say that it could be done more efficiently by FFT methods (which involved padding), and there was a long history. In fact someone characterised it as a Lomb periodogram, and it is certainly of a class of Least-squares spectral analysis (LSSA).
In the most recent version, he is using regression of the data onto sinusoids, and investigating the effect of using monthly or annual time divisions. Tamino chimed in in a positive spirit (the thread was called "Well, Color Me Gobsmacked!"), and said the method was known as the Date-Compensated Discrete Fourier Transform.
I think Willis now regards the chief advantage of the method as allowing for irregularly spaced data, in his case missing months, and that is what the DCDFT is for.
The method is sometimes being criticised as not being a truly orthogonal decomposition. I think that is misplaced. You can look for periodicities in a Fourier decomposition, but it is not the only way. I think Willis is basically filtering. He creates the equivalent of a perfectly tuned circuit, which takes the data as input, and identifies the amplitude of the response as the measure of periodicity. I think that is fine, and so I'd like in this post to say how one might assess and maybe improve the merit of that measure.
It's like what you did with the old AM radio receiver. By frequency shifting with a knob, you listened to the sound level to find stations.
What I want to do in this post is to show how you can get past all the issues of missing data and orthogonality, and rephrase in terms of Fourier integrals, which exposes the sources of error. I'm expanding on this comment.
Willis' method as a filter
For any given frequency ω, Willis uses the R lm() function to fit a+b*cos(ωt)+c*sin(ωt). He then returns √(b²+c²) as the amplitude of the fitted sinusoid. He usually plots this against period, not frequency, and looks for peaks.This is a linear filter on the input. Normally we think of a filter as modifying one time series to another. This is a perfectly tuned filter, in that it produces a pure sinusoid as output. That is rather boring, in that it can be characterised by two numbers, amplitude and phase, and Willis drops the phase. But it is still a filter. You can think of it as a tuned circuit (or bell or cavity etc) which responds to frequencies near its resonance.
Expression as an integral
I'll assume that the data represents samples from a continuous function f(t). This assumption is basic to any continuum analysis. You have to assume that the data you have is representative of the values in between. f(t) could, for example, be a linear interpolate.The sum Willis is evaluating in lm() can then be expressed as an integral:
∫ Ψ(t) cos(ωt+θ) f(t) dt
ω is angular frequency, θ phase. All integrals here are from -∞ to ∞, but Ψ(t) is sum of a finite number of delta functions. I've chosen Ψ to suggest a shah (Ш) function, also called a Dirac comb of delta functions. Generally it will here be mostly equally spaced, but that is not a requirement. It is truncated.
So now we can see what kind of filter it is, by looking at the Fourier Transform. The FT of cos is just a paired delta function that shifts the spectrum of Ψ(t) to center on ±ω. So if Ψ has, say, N=200 delta functions with s=1 annual spacing, the Fourier transform (t origin at the middle) is
sinc(Nω)/sinc(sω)
where sinc(x)=sin(x)/x
It looks like this in the frequency domain:

and the amplitude looks like this:

It is symmetric about 0. When combined with the sinusoid, it is displaced. Willis is looking for periods around 10 years; using that as a test frequency gives:

I think this shows a number of things. There is a peak at 1/10 yr-1. It has side lobes, which represent the effect of the finite (200 yr) interval. These affect the ability to discriminate peaks. It is actually periodic overall, with period 0.5 yr-1 (the FT alternates in sign and has period 1 yr-1). That shows problems when you get up to the Nyquist frequency. But the peaks are fairly sharp, and the Nyquist troubles far away, at least if you are looking at periods of 10 years or so.
Irregular points
The sinc function ratio is actually the sum of sinusoids evaluated at the sample points. You can evaluate at a set less regularly spaced, with missing values say, and the function won't be radically different. And of course, the method still works.Other ideas
In recent discussion, I've put some other analogies. The method is actually like the way analogue spectral analysis was done. Tuned circuits, acting as filters, responded to the signals in a tuned way. If you aren't familiar with circuits, think of a bank of lossless tuning forks, mounted on a sounding board, say. You buzz the burst of signal, and see which ones pick up the most energy.The mathematics of the regression Willis uses is in fact the math of heterodyning. You multiply by a sinusoid and add. If the signal can reasonably be fitted with a nearby sinusoid, then the trig formula for products will yiekd a beat frequency, lower in pitch as the two frequencies are closer. The addition is a low pass filter, passing with amplitude inversely proportional to frequency. So its response is approximately proportional to both the strength of the periodic component, and to its closeness.