Calculating the environmental lapse rate

I have posted over the years on the mechanisms of the lapse rate - the vertical temperature gradient in the atmosphere. It started with one of my first posts on what if there were no GHE. My basic contention has been that lapse rates are a consequence of vertical air motions in a gravity field. Wind tends to drive the gradient toward the DALR - dry adiabatic lapse rate = -9.8 °K/km. Maintaining the gradient takes kinetic energy from the wind to operate a heat pump. The pump forces heat down, to make up for the flux transported up by the gradient. The pump effect is proportional to the difference between the actual lapse rate L_a and the DALR L. L is the stability limit, and a steeper gradient will convert the pump into an engine, with convective instability. This also pushes L_a (down) toward L.

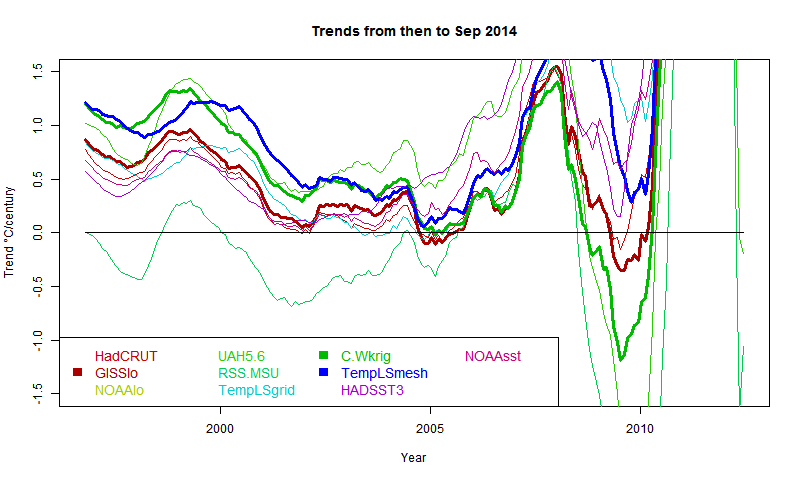
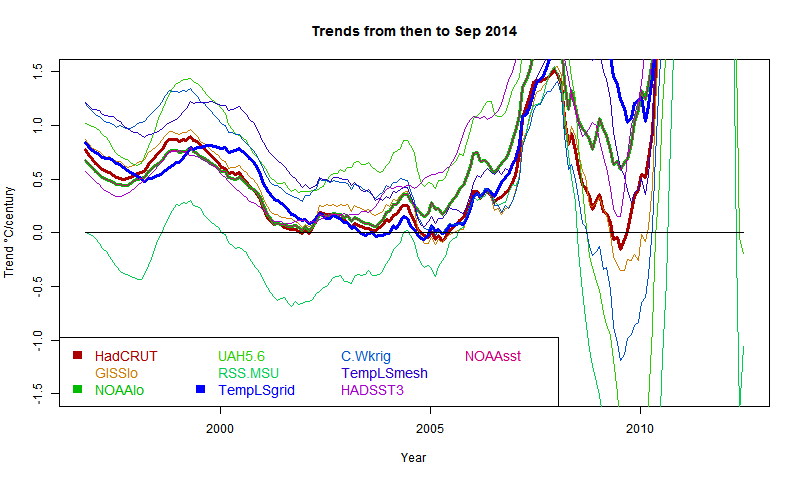
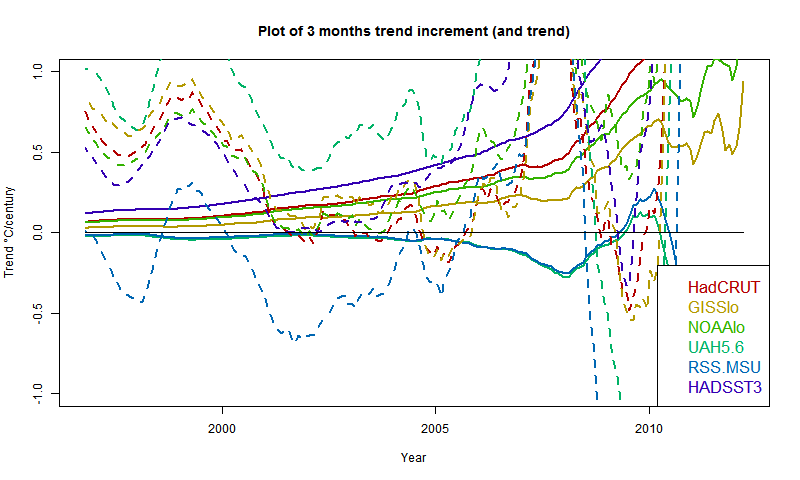
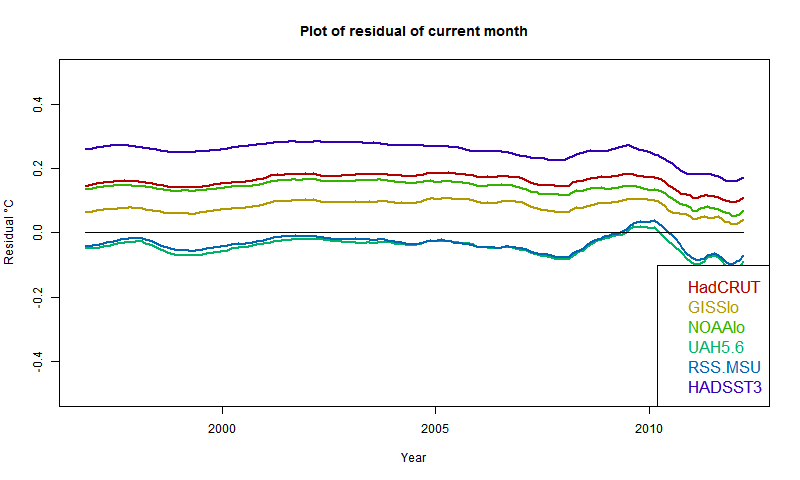
I developed these ideas in posts here, here and here. But I have wondered about the role of infrared radiation (with GHGs), and why the actual gradient is usually below the DALR. The latter is often attributed to latent heat of water, and called the moist ALR. But that is only effective if there is actual phase change (usually condensation).

I now see how it works. The heat pump reduces entropy, proportionally to the energy it takes from the wind. The entropy can indeed be related to the gradient and the effective thermal conductivity; the largest component of that is a radiative mechanism. So the lapse rate rises to the maximum level that the wind energy can sustain, given the conductive leakage.

I'll write a simplified argument first. Consider a parcel of dry air, mass m, which rises vertically dist dz for a time, at ambient pressure P=P_a, starting at ambient temperature T=T_a. The motion is adiabatic, but it then comes to rest and exchanged heat with ambient.

The temperature inside the parcel drops at the same rate as the DALR, so the difference : d(T-T_a)/dz = -(L-L_a)

The density difference is proportional to this
d(ρ-ρ_a)/dz = -(L-L_a)*ρ/T
I'm ignoring second order terms in dz.

The net (negative) bouyancy force is
F = V g (ρ-ρ_a)
dF/dz = -V g (L-L_a)*ρ/T

The work done against bouyancy (power) is ? F dz = 1/2 V g (L-L_a)*ρ/T dz²

Note that this is independent of sign of z; the same work is done ascending as descending.

Because the temperature on arrival is different to ambient, heat has been transported. I could work out the flux, but it isn't very useful for macroscopic work. The reason is that not only is it signed, but separate motions convey heat over different segments, and there is no easy way of adding up. Instead, an appropriate scalar to compute is the entropy removed. Heat pumps do reduce entropy; that's why they require energy. Of course, entropy is created in providing that energy.

The simplest way to calculate entropy reduction is to note that the Helmholtz Free Energy U - TS (U=internal energy) is unchanged, because the motion is adiabatic. This means T dS and P dV (pressure volume work) are balanced. And P dV is from the buoyancy work. So:
T dS = -1/2 m g (L-L_a)*ρ/T dz²
where S is entropy

Going macro

I've shown the work done and entropy generated by a single movement. I'll try to relate that to a continuum. I've used a particular artificial example to link work done with entropy removed. In fact, turbulence typically consists of eddy motions.

Assume there is a distribution of vertical velocity components v in a slice height dz. I can then re-express the work done as a power per unit volume: F v = 1/2 v.dx' g (L-L_a)*ρ/T
In Latex I'd use hats to indicate averages.

I've left in a dx' which was the old distance of rise, which determines the average temperature discrepancy between parcel and ambient. It's not obvious what it should now be. But I think the best estimate for now is the Prandtl mixing length. This is related to the turbulent viscosity, and in turn to the turbulent kinetic energy (per unit volume) TKE.

So now it gets a bit more handwavy, but the formula becomes
Average power/vol (taken from wind) ~ -g (L-L_a)/T * TKE

This follows through to the rate of entropy removal, which is

rate of entropy ~ -g (L-L_a)/T² * TKE
(power divided by T)

Temperature gradient as a source of entropy

If you have a steady temperature gradient, and a consequent heat flux Q determined by Fourier's Law:
Q = -k dT/dz
where k is a conductivity,
then the volume rate of creation of entropy is
dS/dt = -Q d(1/T) = -Q/T²dT/dz
= k L_a T^-2

So what is k?. Molecular conductivity would contribute, but where GHG's are present the main part is infrared, which is transferred from warmer regions to cooler by absorption and re-emission. In the limit of high opacity, this follows a Fourier law in the Rosseland approximation
flux = 16 s G n² T³ dT/dz
s Boltzmann's constant, G an optical parameter (see link), n refractive index. Three optical depths is often used as a rule of thumb for high opacity; we don't have that, but you can extend down by using fuzzy boundaries, where for eample there is a sink region where there is transmission direct to space.
Update: I forgot to say the main thing about G which is relevant here, which is that it is inversely proportional to absorptivity (with an offset). IOW, more GHG means less conductivity.
Update
I've made an error here. I assumed that the flow expansion was adiabatic. This is conventional, and relates to the time scale of the motion. But I've also assumed adiabatic for the entropy balance, and that is wrong. There is a through flux of energy, mainly as IR, as indicated. And that flux carries entropy with it. So the formula should be:
dS/dt = (k L_a - Q) T^-2
where Q is the nett flow of heat. I'll correct below. It is significant, and may change the sign.

Balancing it all - lapse rate determined

Now we have an entropy source term and a sink term. In steady state entropy can't accumulate, so they balance:
k L_a T^-2 ~ g (L-L_a)/T² * TKE
or
L_a - L ~ - (k L_a - Q)/g/TKE
Obviously, there is an unspecified constant of proportionality (with time units), which comes from the nature of turbulence. But I don't think it should vary greatly with, say, wind speed.

So what can we say about the discrepancy between environmental lapse rate L_a and theoretical DALR L (=g/c_p)?

• Proportional to k, the conductivity. So if GHGs transport heat in response to the temperature gradient, as they do, the lapse rate diminishes, away from L. With no GHG's, there is much less to separate L and L_a. Not so clear - see above correction.
• Inversely proportional to TKE (depends on wind speed). So stronger wind brings the lapse rate closer to L
• Proportional to (L_a -Q/k).

So what about moisture? That is what the difference between L_a and L is usually attributed to.

I think moisture is best accounted for within the DALR formulation itself. The DALR L is, again, L= -g/c_p, where c_p is the specific heat of the gas (air). But in the derivation, it is just the heat required to raise the temperature by 1 °C(OK, that is what sh means), and you could include the heat required to overcome phase change in that. That increases c_p and brings down the lapse rate. The thing about the moist ALR is that water only has a big effect when it actually changes phase. That's a point in space and time. Otherwise moist air behaves much like dry. Of course, an environmental lapse rate is only measured aftre there has been much mixing

Checking ENSO forecasts

I few days ago I commented here on the latest NOAA ENSO advisory:
""ENSO-neutral conditions continue.*
Positive equatorial sea surface temperature (SST) anomalies continue across most of the Pacific Ocean.
El Niño is favored to begin in the next 1-2 months and last into the Northern Hemisphere spring 2015.*""

I repeated this at WUWT, and someone said, but they have been saying that all year. So I ran a check on ENSO predictions.

The NOAA Climate Prediction Center posts a monthly series of CDBs (Diagnostic Bulletins) here. They are full of graphs and useful information. They include compilations of ENSO predictions (Nino3.4), nicely graphed by IRI. I downloaded the plots for each month of 2014, and overlaid with the observed value from this file.

It's an active plot, so you can click through the months. The year started out with a dip, mostly unforeseen. This coincided with the global cool in February. There was then a underpredicted recovery, and since then there has been a tendency for the index to be below predictions, esp June and July.

CPC warns that only modest predictive skill is to be expected, and that is fortified by the spread in forecasts. The index does indeed seem to move beyond the predicted range rather easily. It's not always overpredicted, though.

Here is the active plot. Just click the top buttons to cycle through the 9 months. The thick black overlay line are the monthly observations.


You'll see some minor discrepancies at the start. I don't think this is bad graphing - I assume minor changes to Nino3.4 between the monthly report and now. It looks like maybe a scaling error, but I don't think it is. I should note that I'm plotting the monthly value, while the foecasts are for three minth averages. I wanted to match the initial, which is one month. But Nino3.4 does not have much monthly noise, so I don't think averages would look much different.

More "pause" trend datasets.

In two recent posts (here and here), I have shown with some major indices how trends, measures from some variable time over the last two decades and now, have been rising. This is partly due to recent warmth, and partly to the shifting effect (on trend) of past events, as time passes.

This has significance for talk of a pause in warming. People like to catalogue past periods of zero or negative trend. A senior British politician recently referred to "18 years without warming". That echoes Lord Monckton's persistent posts about MSU-RSS, which does have, of all indices, by far the lowest trends over the period.

Here I want to show results about other indices. Cowtan and Way showed that over this period, the trend in Hadcrut was biased low because of non-coverage of Arctic warming. I believe that TempLS with mesh weighting would also account properly for Arctic trend, and this would be a good way to compare the two, and see the effect of full interpolation. I expected GISS to behave similarly; it does to a limited extent.

So a new active plot is below the jump. You can rotate between datasets and months separately. There is also a swap facility so you can compare the images. And I have individual discussion of interpolation data vs grid data groups.
Here is the main plot. Buttons to rotate months and datasets. Emphasised set is in thicker black, on the legend too. (For some reason, NOAA emphasises as red). There is a reserved group of images for which the swap buttons work. It's initially empty, and you need at least two. In non-swap mode, click push to add the current image. In swap mode, click pop to remove the currently visible from the set.

Data	Month	Swap

General comments much as before. There is a big contrast between satellite indices MSU-RSS (long pause) and UAH (short). Trends are rising as the months of 2014 progress. I'm extrapolating to November assuming continuation of current weather, as described in previous posts. Trends are generally rising, which means it is getting harder to find long periods of non-positive trend ("pause").

Interpolation groups

As Cowtan and Way found, whether or not you see a pause depends a lot on whether you account for Arctic warming. TempLS typifies this - the grid version, like HADCRUT, effectively assigns to empty cells (of which Arctic has many) global average behaviour, missing the warming. TempLS mesh has full interpolation, like the kriging version of Cowtan and Way. So here is the comparison plot, with C&W, TempLS and GISS in dark colors:

It shows C&W and TempLS tracking fairly closely from 1997 to 2008, with GISS generally a bit below.

Grid surface data

And here for comparison are HADCRUT, NOAA Land/Ocean and TempLS grid. I expect these to be fairly similar. TempLS and NOAA have been very close lately, but over this longer range, TempLS is closer to HADCRUT.

External sources

HadCRUT 4 land/sea temp anomaly

GISS land/sea temp anomaly

NOAA land/sea temp anomaly

UAH lower trop anomaly

RSS-MSU Lower trop anomaly

Cowtan/Way Had4 Kriging

HADSST3

NOAA sea temp anomaly

Tails of the Pause.

I've been writing lately about matters which, I'm sorry to say, lack scientific gravity. One is the possible record warm 2014, and the other is the tailing of the Pause, as measured by periods of negative trend. My excuse is, people do talk about them, and there is interesting arithmetic which I can illustrate.

In my "pause" posts, I showed plots of trend of global temperature to present, plotted for periods shown on the x-axis, with trend shown at the starting point. A "pause" starts when, for some index, the axis is first crossed from pos to neg. The plots were active, and you could see the curves rising steadily over recent months. This meant the start of the pause moves forward, with eventual jumps where a previous excursion below the line no longer makes it.

Here is the recent active (buttons) plot to show that effect:


In this post, I'll quantify the rate of motion, and describe how much cooling would be required to reverse the trend. The effect of a new month's reading depends on its status as a residual relative to the regression line for the period - ie is it above or below the line, and by how much. But one reading is a different residual for each such period. I plot the present month as a residual, again referred to the start year, and also plot the rate of change of trend produced by the current (August) temperatures.

Rate of change

This is more simply described with a continuum version. A time period runs from 0 to x, with readings y. If x increases, what is the change to trend β. The continuum formula is β = (x ∫ xy dx - x*x/2 ∫ y dx)/(x^4/12)
Note that y occurs only in integrals (which are from 0 to x), so when we differentiate β, no need to differentiate y. So, after some calculus algebra,
dβ/dx = (6/x^2)(y - y0 - βx/2)
where y0 is the mean over the period. Since the regression passes through this mean midway, the last part of this is the end residual.
ie dβ/dx = (6/x^2) * residual
That gives the factor that determines the rate.

So my first plot is the rate of rise, shown as a 3 month incrementwith August trends dotted



The satellite measures aren't going to move much without substantial warming. However, UAH is already high, RSS is low. Of the surface indices, HADSST3 is rising fast, GISS relatively slowly. However, three months of current warmth makes a big difference to the pause.

And here is the plot of residuals of August temp relative to past regressions:



It confirms that UAH and RSS are near zero, so continuation of present temps won't change anything (though UAH warmed in Sept). Otherwise, GISS has the lowest residual, but positive everywhere; HADSST3 the highest. This of course partly reflects past coolness of HADSST3.

So if temperatures drop about 0.07°C from August, the rise for GISS would pause (but GISS rose in September). It would take a drop of more than 0.2°C for HADSST3.

Record warmth in 2014?

Not according to the satellite measures; they are showing quite a cool year so far. But surface measures, apparently propelled by SST, have been consistently high since March, and a record for calendar 2014 looks possible.

In August 2010, I showed a plot of the progress of the cumulative monthly anomaly sums, which will reach the final sum that determines the year average. 2010 did turn out to be the hottest year in many indices. It was different in that the El Nino was late 2009/10, so late 2010 was cooling. At this stage 2014 seems to be warming.

So I started to repeat that 2010-style plot, which is below the jump. It didn't work as well; the variation doesn't much show. But it puts the thing calculated in context - a cumulative sum that, if it exceeds 2010 at year end, will set a record. I've shown the progress of 2005 (a previous record), 2010 and 2014, with a line showing the 2010 average rate. The plots are spaced with an arbitrary offset.

But, more effectively, there is then an active plot with the average 2010 trend subtracted. The variation is clearer. The key thing is not so much whether the current total is above the line, but how it is trending, which is a measure of current warmth.

So here is the first plot. The TempLS measures were described in this recent thread. The absolute slope is an artefact of the anomaly base - GISS is earliest.



And here is the active plot with the 2010 average subtracted. Use the buttons to click through.




NOAA and TempLS grid are already above the line and heading up. Top candidates for a record. HADCRUT looks likely too. GISS and TempLS mesh only need a reasonable continuation of current warmth to end up positive (record). The slope is positive only when a month exceeds the average for 2010, so it doesn't take much cooling to turn down. We'll see.

QC for TempLS

I plan to do more with TempLS (see last post) so I want a stable quality control (data) scheme. GHCN unadjusted is a document of record, and there is weird stuff in there which it seems they don't like to touch. I've noted current examples earlier in the year. So I did a survey of the data since 1850. Here is R's summary of the monthly averages:

Min.	1st Qu.	Median	Mean	3rd Qu.	Max.	NA's
-87.0	6.6	15.9	14.5	24.1	154.4	1166444

That's out of 10349232 months (of years with some data). Yes, the max is 154.4°C. There were 28 months with a min/max (not max) average >50°C.

To be fair, they use flags, and these oddities seem to be mostly where a decimal point slipped in the originating data. But they are big enough to have effects, so I have been using my own QC. On first look, I found the GHCN flags numerous and unhelpful, so I used a scheme where I checked with the adjusted file. This seemed to weed out the problem points without replacement. However, it excluded a lot of other points, so I allowed those if within 3°C of the appropriate mean.

I did that for the last five years of data and it worked well enough. But then I thought I should try for the whole record. I worked out how to extract the QC flags; here is a table of their occurrence:

	D	L	M	O	S	W
5511098	1124	647	22	3904	5448	1981

The first column is no flag. QC flags aren't that common, about 0.24% of the total. The letters mean, according to the readme:

• D - apparent duplicate
• L - isolated
• M - manual
• O - outlier (>5 sd)
• S - not so outlier (>2.5 sd), but no nearby data in agreement
• W - seems to be last month

O and S are the big ones, and as expected, the very high ones are flagged O.

So I decided to just omit all flagged data. In future, I'll do that to all GHCN unadjusted before use.

If you've been watching the latest data over the last day, you'll have seen me experimenting. I think it is stable now.

A catch-up on TempLS

I've been writing a lot about TempLS (my global temperature index) recently, and realizing that I don't have a unique reference that explains exactly what it is and what has recently been happening to it.

TempLS dates back to a period in early 2010 when there was a flurry of amateur efforts to replicate the monthly global surface temperature indices from the major producers (which some thought suspect). This post by Zeke (with links to earlier) gives an overview. Jeff Id and Romanm started it with a reconstruction that used a least squares method for aggregating a single cell, yielding offsets rather than requiring a fixed anomaly period. I thought that could be applied to the whole recon.

So I developed TempLS, which was basically a big OLS regression, based on GHCN unadjusted station monthly averages. It was quick to run, and I incorporated choice mechanisms which made it easy to calculate regional or special (eg rural, airport) averages. A rather complete summary of this stage of development is here. An important feature was the incorporation of SST data. This comes gridded, often 5°x5°, and so I simply entered these as stations.

I made a point of using unadjusted GHCN, because there were many claims that warming was an artefact of adjustment. I have myself no objections to adjustment, though I did show that it makes relatively little difference to the index.

TempLS combines weighted regression with spatial integration, much as BEST did later. It weighted initially by the inverse of grid density, estimated by stations/cell in a 5°x5° grid. I posted at one stage a very simple version for incorporation in Steven Mosher's RGHCNv3. You can regard this weighting as that which a spatial integration formula woud provide, with each grid estimated by its station average anomaly, or equivalently, each function value (observed average) assigned an area equal to its share of the cell.

Version 2 in August 2010 generalised the idea of regression, so that spatial variation (among others) could be included (and maps produced). The math basis was set out here.

Meanwhile I was experimenting with other kinds of weighting. The problem with cell averages, which I now cell grid weighting, is that many cells have no stations. These would be best represented by local data, but the weight that can be assigned is limited to one cell area, and near the poles, where there is a lot of sparseness, the cell areas actually diminish, so such regions are under-represented. In early 2011, I did a series on Antarctica (final and links). This developed various forms of mesh-based weighting. This means that every point is estimated based on local data. I tinkered with Voronoi tessellation, but have now settled with weighting that assigns to each node a weight equal to a third of the area of the triangles (from a convex hull, which provides an irregular triangular mesh) which touch it. This is equivalent to a finite element piecewise linear integration formula.

An interesting exercise, which I started in early days, is to see if some very small subset (60) of stations can give a reasonable world estimate. This is the latest in that series, with links back.

Version 2.1, which incorporates some revised verion, is described here. This is the last formal release with code.

Meanwhile, in July 2011 I started a regular cycle of posting a monthly average estimate, based on GHCN and SST - initially HADSST2, but I soon switched to ERSST. I tried to make sure to post ahead of the majors, so that a prediction record could be established. I then published a comparison with the GISS result for the month. A list of links to those posts is given here; each has a list to its preceding TempLS post. I also included the TempLS results with the other indices on my latest data page, and in the graphical comparisons there.

I posted a review of the comparison of TempLS with other indices in December 2012. It was clearly in the mainstream, closest to NOAA and HADCRUT. More recently, I posted a mini-review noting that the closeness to NOAA had become more pronounced.

I had thought of switching to mesh weighting for regular monthly, but was deterred by the hour+ it takes to do 1200 meshes to cover a century. But you don't need a new mesh each month; most historic months change the population of stations very rarely. So with a scheme of stored weights and detecting changes, I can do it, and I think I should. I expect the results to be now closer to GISS. I also expect that the results will compare well with the revision of Cowtan and Way; I'll post on that soon.

Appendix/Update

Carrick asked for more details on the use of meshes in integration. The FEM idea of integration is that you build up an interpolation which is exact at each node, and takes some polynomial form in between. They do it with basis functions, but we don't need to deal with that here. Just imagine that you have a linear interpolation on each triangle. They will match at the edges.

On the integration, first I'll formalize the trapezoid analogy. If you have two points z1,z2, with function values f1,f2, then the area of the trapezoid on the graph for the linear interpolation is (z2-z1)*(f1+f2)/2. Base length times mean height.

The corresponding formula in 3D is volume = base area * (f1+f2+f3)/3.

To prove it, let the linear approx be f=a.z+c. (a,z,vecs, . scalar product). Then f1 = a.z1+c etc.

To save writing determinants I'll invoke what I hope is a familiar proposition. The centroid z0=(z1+z2+z3)/3 is also the center of mass. ie ∫ z dA = z0 A, where A is the area of triangle (z1,z2,z3).

So ∫ f dA = a . ∫ z dA + ∫ c dA = (a . z0 + c)*A
= A * Σ_i ( a . z_i + c)/3 = A * (f1+f2+f3)/3

Now when you collect all the formulae for each triangle (FEM assembly), you get a big sum in which each node value f_i is multiplied by 1/3 of the sum of all the areas of triangles of which it is a node. That is the weighting I use (actually, no need to divide by 3).
<

GISS September 0.77°C, up by 0.08°C

This my first report in the new style, where I record details of both mesh-weighted and traditional grid-weighted TempLS, along with the latest GISS. It is part-mechanical, but I annotate. TempLS numbers on the latest data page are constantly updated, but the monthly reports here won't change.

So the headline is, a very warm month. I think in GISS at least, 2014 may well be a record year. TempLS mesh showed a similar rise; TempLS grid dropped slightly. I expect the mesh version to more closely follow GISS, and the grid version to continue tracking NOAA. My next post will probably be an updated explanation of TempLS.

I've given both TempLS maps below. You can see again that TempLS mesh is closer to GISS than grid.

Comparison of GISS and TempLS, Sun 12 Oct 2014

Anomaly °C	Apr	May	Jun	Jul	Aug	Sep
GISS	0.71	0.78	0.61	0.52	0.69	0.77
TempLS mesh	0.641	0.669	0.58	0.477	0.627	0.673
TempLS grid	0.612	0.607	0.58	0.515	0.615	0.598

Anomaly base years: GISS 1951-80, TempLS 1961-90.

Here is the GISS map


Here is the spherical harmonics based plot, mesh weighting


Here is the spherical harmonics based plot, grid weighting


List of past reports

New ideas on TempLS reporting - mesh

For over three years now, I've been running my least squares based GMST index TempLS each month and reporting the results, with a second post comparing with GISS. See here and here for last August. The second has past links. I did a mini-review here recently, and there is a new summary of TempLS here.

I'm planning a change. For some time, I've believed that using mesh based weighting (see here and here, for example) is better than what I call grid-based weighting, where observations are weighted on a cell-based density estimate. I was deterred from changing because the mesh generation took a long time, but I've fixed that. I'll persist with the grid model because as I noted, it has uncanny agreement with NOAA, and also tracks HADCRUT well. But I think that it also has the faults of those, in dealing with empty cells. For TempLS it takes the form that stations in empty areas have a capped weight based on the size on one cell, which in the Arctic can be small.

The data cycle goes like this. ERSST posts a preliminary on about 3rd or 4th of month. It's actually complete, and the numbers are little different when updated in late month. GHCN starts the month with a rush of numbers from places with efficient electronic systems, and then stuff trickles in fairly slowly. Lately GHCN (unadjusted) has had early gyrations too. But notwithstanding, I think it is meaningful to to a mesh baed calc as soon as the SST comes in. Mesh is more robust to missing.

I've now posted an automatic report on the latest data page. It shows the current mesh-based report, with maps of temperatures and of reporting stations. I think I can maintain this, reporting with every new GHCN (most days). It would flip to the new month when the SST is posted. Obviously, early figures would be subject to change.

This would supersede my first monthly report on the grid results. I'd still publish the GISS comparison, and record the grid and mesh TempLS results there.

Update. GISS has produced a map for September, and it says the Sept temperature is 0.78°C, up from 0.70°C in August. This tracks the mesh TempLS rise from 0.628°C to 0.673°C (grid TempLS went down slightly). I expect that mesh TempLS will follow GISS more closely. I'll post the GISS comparison soon. The new number is not yet on their datafile. It's getting warm.

TempLS global temp down 0.017°C in September

TempLS cooled slightly; from 0.615°C (July) to 0.598°C. That is still quite high, following the previous rise of about 0.1°C. Anomaly base is 1961-90. For the satellite indices, MSU rose slightly, and UAH quite a lot, from 0.19°C to 0.29°C.

GHCN had ups and downs lately. For a few days, almost all the land data for August except USA vanished. In Sept, China data has only just arrived. I think everything is OK now.
Here is the spherical harmonics plot:


Warm in Antarctica, around Paraguay and Algeria. Cool in mid-Russia.
4273 stations reported. Here is the map:

Portal for GHCN Daily

Many people are aware of GHCN Monthly. This is the large compilation of station monthly averages used for making global indices. I posted a portal here. Fewer know about GHCN daily, which is a very large compilation of daily records. Partly because of its size, it is less accessible. Each station record is in a separate file, and even listing the "all" directory takes a long time.

It is far less organized than GHCN Monthly. Many records are very short and incomplete. There is a mixture of TMAX, TMIN, precipitation, and various things like snow. Not easy. It is, however, for those who like that sort of thing, unadjusted. Very raw data.

So I've organised some links. I've split into US1, USC, Australia, Canada and others. US1 seems to have little or no temp data. USC is basically the Co-op network. The Australia record is huge, but a lot is rainfall. Canada is also large. So I've broken down those by states, and other countries are in the "World" list. Even there, some very significant countries are in the "Other" group at the end. Coverage is very uneven.

I've marked the files that have temp data (well, TMAX) with the years of record. As I mentioned, these can be short, and full of gaps at that. Entries without years probably don't have temperature. On the "Other" list, I've also marked where each country block begins.

So it's below the jump. You request by selecting from one of the menus. Clicking on a link will make the actual record pop up in a separate window or tab. I'm planning to create a permanent page for the various portals.

Update: I've added buttons that with Chrome will force the selection to take effect.

US1

Rising Trends

About a month ago, I wrote a post about how trends of global temperature calculated over recent past periods had been rising, and the periods of zero or negative trend, commonly quoted as evidence of the "pause", were likely to diminish rapidly if warm weather continued.

The weather has been warm, and with another month of data, that process has continued. I'll show the active plot below, in which you can see how the trends calculated over various periods back from now have changed since March, and are likely to change in the next three months if current warmth continues.


There has been a change to HadCRUT data since the last report. A new version of HadSST3 caused subsequent changes in HadCRUT4. I believe that are also fewer empty cells in HadCRUT4, which will help remove the cooling bias that Cowtan and Way identified. The changes to both HadSST3 and HadCRUT4 are noticeable.

In the active plot below, you can use the arrows to cycle through the months from March to November. Future data is padded by reflection - September is the same as August, October as July etc. In fact we have data for MSU and UAH in September. MSU was about the same, UAH a bit higher. I stuck with the padding for this post.

As before, what is plotted is, for each date, the trend of temperature from that date to August 2014. Of interest for pause talk is where the curves cross the x axis.

Analysis of short-centered PCA

There has been a lot of to and fro (see recent posts) about short-centered PCA - MBH style (background). My general view here is that there is an effect on the first principal component, but that merely moves to a particular alignment of basis vectors, and doesn't affect any reasonable reconstruction. And it all happened so long ago...

But still it's an interesting analytic problem, so I did some analysis. It particularly concerns the role of persistence, or autocorrelation. Increased autocorrelation tends to show more effect, because for a given number of proxies, it diminishes the effect of noise relative to the underlying short-centering operator (graphs below). But that underlying pattern is interesting, because it is much less dependent on autocorrelation. And the next PC's in succession are interesting, as I wrote about here.

White noise

You need an infinite quantity of proxies to see a pattern with white noise. But the pattern is the prototype for more difficult cases, so I'll develop it first. Much of what I have done recently is based on the work in the NAS report and its associated code. They compute and scale not only PCA first components from AR1() proxies, but also from the associated correlation matrices, which they scale and put on the same graph.

The algebra of short-centered averaging works like this. Define a N-vector h which has zeroes outside the short averaging period (M years at the end of N years of data), and values 1/M within, and another vector l which has 1's only. Then for a data vector x, length N, the valkue with short mean deducted is x-l*(h.x), or E*x, where E=I-l⊗h. I is the identity matrix, and ⊗ the dyadic product. For future reference, I'll note the dot products
l.l = N, l.h = 1, h.h = 1/M.

Then for a data vector X, Nxp, p the number of proxies, the PC's are the eigenvectors of XX^*. The expected value of this, as a random noise vector, is p*K, where K is the autocorrelation matrix. For eigenvectors we can drop the p. The short-averaged version is E*X*X^**E^*. So for white noise, K is the identity I, and we need just the eigenvectors of E*E^*.

Expanding, the eigenvalue equation is
(I-l⊗h - l⊗h + l⊗l h.h)*u = z u
or
(l⊗h + l⊗h - l⊗l h.h) u = (z-1) u

Since the matrix on the left now has range spanned by l and h, u must be in this space too. So we can set u = A*h+B*k, and there is a 2-dim eigenvalue for u in this space. I'll skip the 2-d algebra (just substitute u and work out the dot products), but the end results are two eigenvalues:
z=0, u=l
z=N/m, u= l-h
The latter is clearly the largest eigenvalue. There are also a set of trivial eigenvalues z-1=0; these correspond to the remaining unchanged eigenvalues of I.

So what has happened here? The short averaging has perturbed the correlation matrix. It has identified the vector u=l-h, which is 1 for years in 1:(N-M) and zero beyond, as the first principal component. This will appear in any reduced set of eigenvalues. All vectors orthogonal to it and l are still eigenvectors. So no new eigenvectors were created; u had been an eigenvalue previously. It just means that now whenever a subset is formed, it will come from a subset of the unperturbed set. They were valid bases for the space before; they still are.

Effect of autocorrelation.

I showed earlier DeepClimate's rendering of two AR1() cases from the NAS code:

AR(r=0.2), 5 PC1s from sets of 50 proxies.	AR(r=0.9)

You can see that relative to the HS effect, the noise is much greater when r=0.2 (it depends on proxy numbers). And I can't usefully show white noise, because the noise obliterates the effect. but the eigenvector is not very different.

Here are some plots of PC1 from r=0.1 to r=0.9. I've kept to the same scale. You can see the gradual change in the matrix eigenvector, and the gradual downscaling of the noise, which makes the eigenvalue pattern stand out more.

Next

My main ambition here was to get theoretical expressions for these eigenvalues. It is possible, and interesting, to convert the eigenvalue equation to a difference equation, which emphasises the Sturm-Liouville pattern for higher eigenvectors. For PC1, it just gives an expression for the rounding that you see. That's for another day.