Station-based monthly global temperature indices use gridding at some stage, and usually the grid cells follow some regular rule, like a lat/lon square. This causes some problems:
- Minor - cells are unevenly populated with stations.
- Major - some cells have no data in some months
These can be avoided with the use of irregular grid cells, which can be smaller when stations are dense, and can be formed with a requirement that they always have at least one data point. |  |
There are needs here which make well-known unstructured meshes like
Voronoi unsuitable. This post describes one based on
binary trees.
The purpose of gridding
The naive way to get a world average temperature anomaly is just to add results for all the stations. But it gives wrong results when stations are concentrated in certain regions. And it underrates SST.
The usual way is to create a regular grid, and in some way average the readings in each cell. Then an area-weighted mean of those cell averages is the result.
This gives a fairly balanced result, and has the same effect as numerical surface integration, with each grid a surface element, and the integrand represented by the cell average.
TempLS does something which sounds different, but is equivalent. It forms a weighting based on inverse cell density, expressed in each cell as cell area divided by the number of data points in the cell.
Another way of seeing that is to imagine that the cell was divided into equal areas, one containing each cell. Then the weights would be just those areas.
Empty cells
Empty cells are usually just omitted. But if the temperature anomaly averaged over just the cells with data is presented as the global average, necessarily some assumption is implied as to their values. If you assumed that each missing cell had a value equal to the average of the cells with data, then including them would give the same answer. So this can be taken to be the missing assumption.
Is it a good one? Not very. Imagine you were averaging real temperature and had a lot of arctic cells empty. Imputing world average temperatures to them is clearly not good. With anomalies the effect is more subtle, but can be real. The arctic has been warming more rapidly than elsewhere, so missing cells will reduce the rate of apparent warming. This is said to be a difference between Hadcrut, which just leaves out the cells, and GISS, which attempts some extrapolation, and gets a higher global trend. GISS is sometimes criticised for that, but it's the right thing to do. An extrapolated neighbor value is a better estimate than the global average, which is the alternative. Whatever you do involves some estimate.
Irregular cells and subdivision
Seen as a surface integral approx, there is no need for the cells to be regular in any way. Any subdivision scheme that ascribed an area to each data point, with the areas adding to the total surface, would do. The areas should be close to the data points, but needn't even strictly contain them.
Schemes like Voronoi tesselation are used for solving differential equations. They have good geometric properties for that. But here there is a particular issue. There are many months of data, and stations drop in and out of reporting. It's laborious to produce a new mesh for each month, and Voronoi-type tesselations can't be easily adjusted.
Binary tree schemes
I've developed schemes based on rectangle splitting, which lead to a binary tree. The 360x180 lon/lat rectangle is divided along the mean longitude of stations. Then the rectangle with longest side is divided again, along the lat or lon which is the mean for stations in that rectangle. And so on, but declining to divide when too few stations would remain in one of the fragments. "Too few" means 2 at the moment, but could be refined according to the length of observations of the stations. There's also a minimum area limit.
That's done at the start. But as we go through month by month, some of those rectangles are going to have no data. That's where the binary tree that was formed by the subdivision comes in. It is the record of the divisions, and they can be undone. The empty cell is combined with the neighbor from which it was most recently split. And, if necessary, up the tree, until an expanded cell with data is found.
Weights
In binary tree terminology, the final set of rectangles after division are the leaves, and adding a notional requirement that for each month each cell must contain data leads to some pruning of the tree to create a new set of leaves, each being a rectangle with at least one data point. Then the inverse density estimate is formed as before - the cell area divided by the number of data. Those are the weights for that month for each cell.
Does it work?
Yes. I've produced a version of TempLS V2 with this kind of meshing. A picture of the adapted mesh for Dec 2008, GHCN, is above. I'll show more.
The mesh manipulations, month to month, take time. I've been able to reduce the run time for a Land/Sea GHCN run to well under a minute, but the irregular mesh doubles that. I'm hoping to improve by reducing the number of tree pruning ops needed.
Results
I did a run from 1979 to 2008. Here are the trends using standard TempLS and the irregular grid version. At this stage, I just want to see that the results are sensible.
| Trend | Reg_grid | Irreg_grid |
| Number | 9263 | 9263 |
| 1979-2008 | 0.1636 | 0.1584 |
| Trend_se | 0.02007 | 0.02119 |
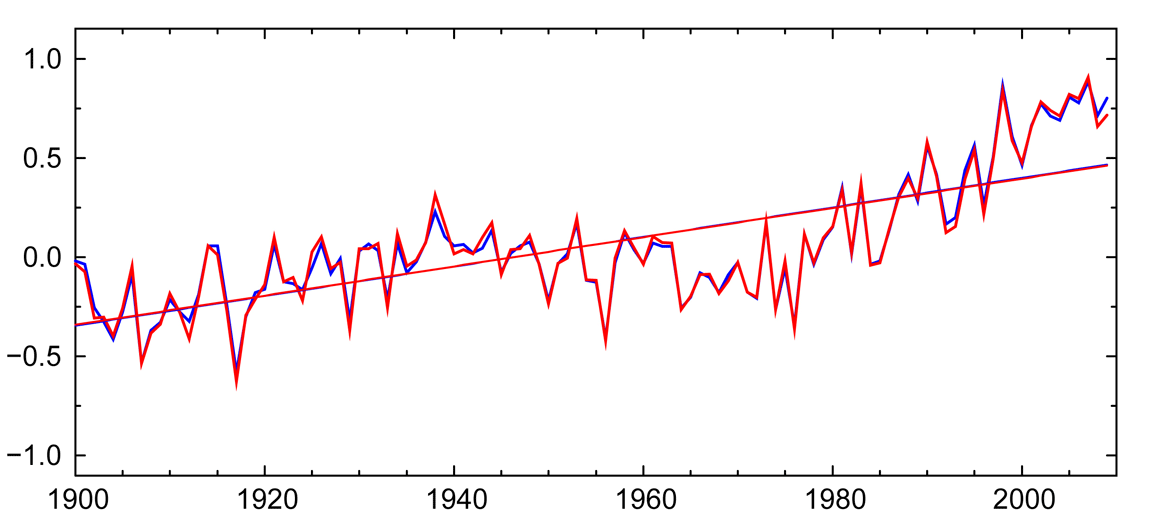
And here is a superimposed plot of annual temperatures:
So what was achieved?
Not much yet. The last plot just shows that the irregular mesh gives similar results - nothing yet to show they are better. I may do a comparison with GISS etc, but don't expect to see a clear advantage.
Where I do expect to see an advantage is with an exercise like the
just 60 stations. I think in retrospect that that study was hampered by empty cells. In fact, almost every station had a cell to itself, which meant they were all equally weighted, even though they were not evenly distributed.
Work is needed to adapt the method to region calculations. If the region can be snugly contained in a rectangle, that's fine. But the surrounding space will, by default, be included, which will overweight some elements.
One virtue of the method is that it has something of the effect of a land mask. With a regular grid, coastal cells often contain several land stations and a lot of sea, and in effect, the sea has the land temperature attributed to it. The irregular grid will confine those coastal stations in much smaller cells.
More mesh views
Finally, here are some more views of that mesh used for December 2008:
The mesh enlargement in the Antarctic seems to overshoot somewhat - it makes large elements with quite a lot of nodes. This should be improveable. There are some big elements in N Canada - this was the period when few stations there were reporting.