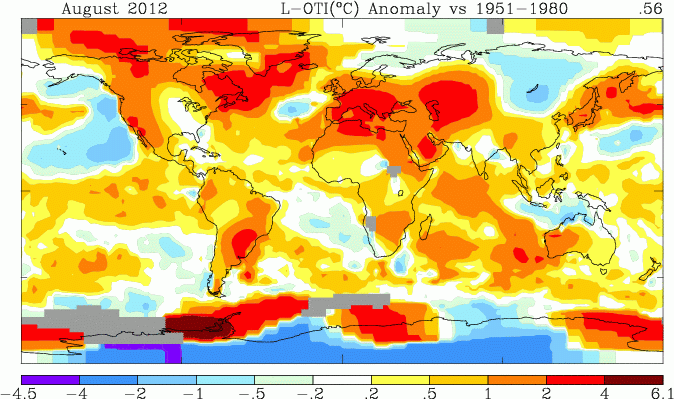
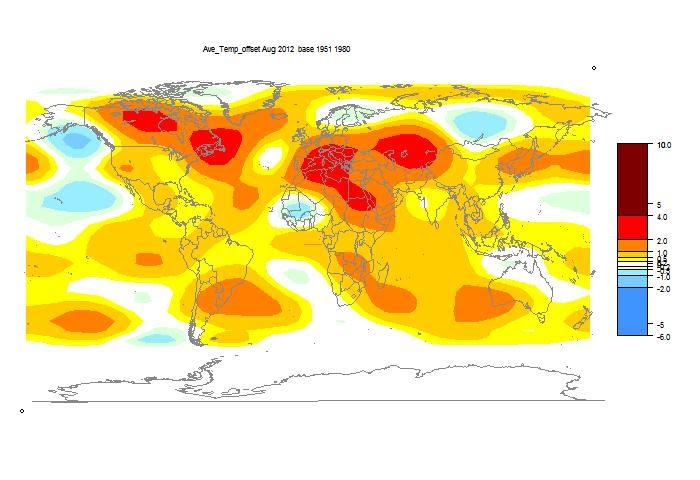
At WUWT, Girma Orssengo, PhD, has a
guest post showing some of the empirical models that he often posts in comments at Climate etc and elsewhere. It shows a parabolic+sinusoid fit to HADCRUT3:

The key plot is the one on the right. It's often been observed that a 60-year (or thereabouts) cycle plus a linear or quadratic does fit in this way. The question is, what does it mean? And in particular, can it be used for prediction?
Girma says that it isn't meant as a basis for
physics interpretation. But when challenged about prediction, he
said:
" Girma says: September 4, 2012 at 12:53 am
Nylo
A model is only useful if it allows predicting future behaviour. I see no predictions by the author that could be later falsified by the real outcome.
The model established a pattern as shown in Graph “f”. From this graph, It is easy to predict the climate if the pattern continues => Little warming in the next 15 years."
So prediction does seem to be an aim.
The problem with curve fitting is that behaviour outside the range is determined by the rather arbitrary selection of basis functions. I tried a regression fit in R using the same basis functions, with similar results:
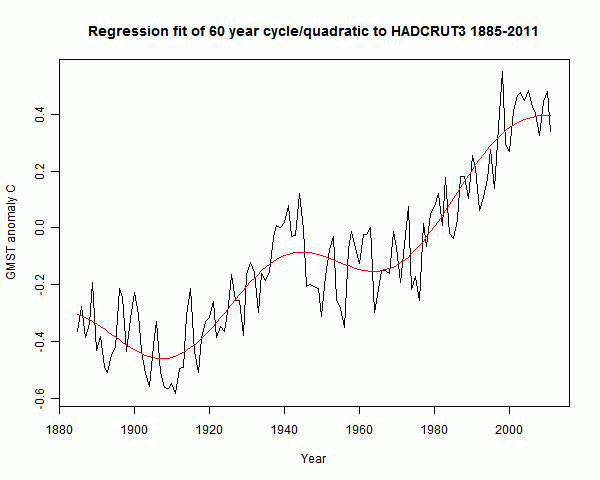
Then I tried the same sinusoid, a 60-year cos function with min at 1910, but instead of t and t
2 I used exp(t/20) and exp(t/100):
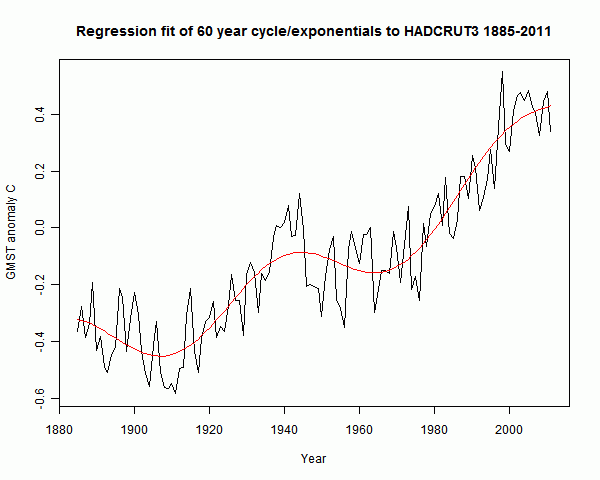
The fit is very similar, and it's not easy to declare that one is better than the other. Here they are on one plot:
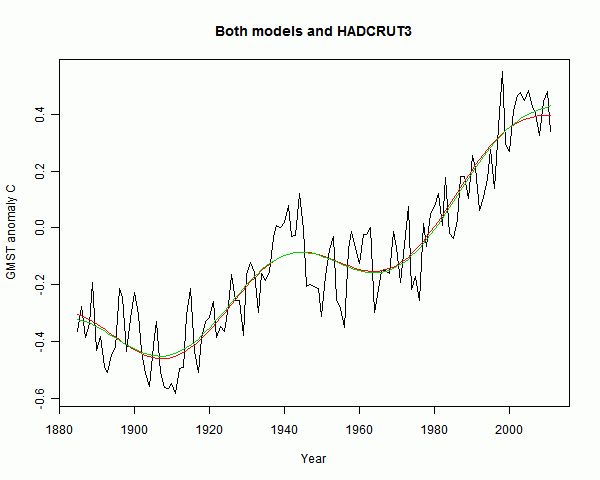
But they give very different predictions. The divergence looking forward to 2050 is not so huge:
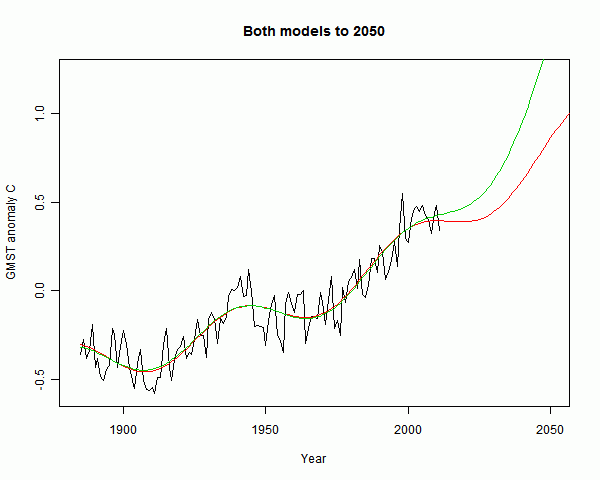
But looking forward to 2100, the exponential model (green) runs right away, warming by 8°C. Grim.
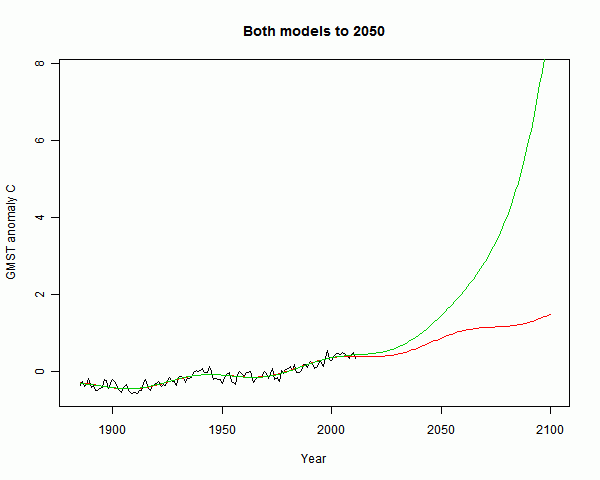
The bind with fancy curve fitting is that it really can't be used much outside the range. And within the range, it isn't telling you anything you didn't already know, unless you are confident that you can make a useful deduction about the physics.
So what about linear regression - very commonly used? Well, it isn't "fancy" curve fitting. But the underlying principle is there. If it is a time series, you need to be open to the possibility that there is a real underlying rate of change. Then regression (curve fitting) can estimate the rate for you. But it doesn't prove that the linear model is right.