Like GISS, Moyhu is coming out with a V4 which will use GHCN V4. Actually, V3 could use it too, but it is time for a new version. GISS has marked theirs as beta - the monthly averages are here. V4 said the rise was only 0.01°C; Moyhu's V4 said the rise was higher, at 0.128°C. V4 of course has many more stations, and somewhat to my surprise, has xtensive reporting quite early; however, there is also extensive later data, and I'm still getting a feel for when it settles. My reporting is mixed; the main table shows V4, but the report and graphs are V3. This will change soon. I'll show below the anomaly maps for Moyhu and GISS V4 as well.
The overall pattern was similar to that in TempLS. W Canada and NW US were very cold, though SE US was quite warm.. Europe was warm, especially NE (Russia). Warmth also in Siberia and Alaska, and nearby Arctic. Australia was still quite warm. I'll note now that March so far is looking a whole lot warmer.
As usual here, I will compare the GISS and previous TempLS plots below the jump.
Here is GISS V3
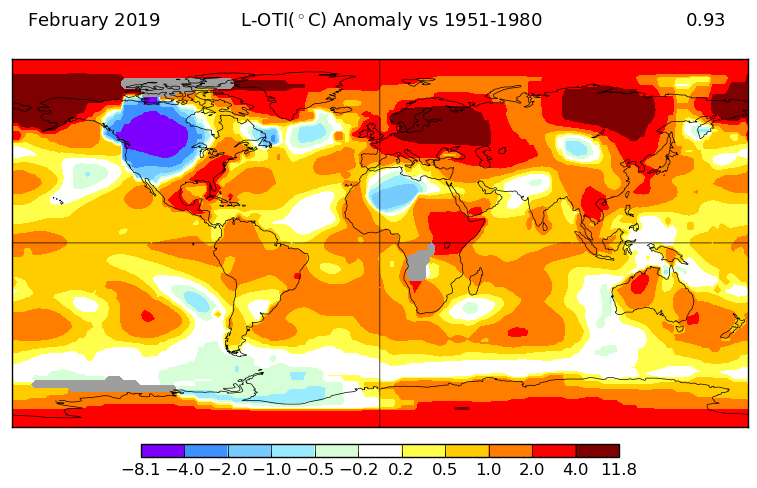
And here is the TempLS V3 spherical harmonics plot
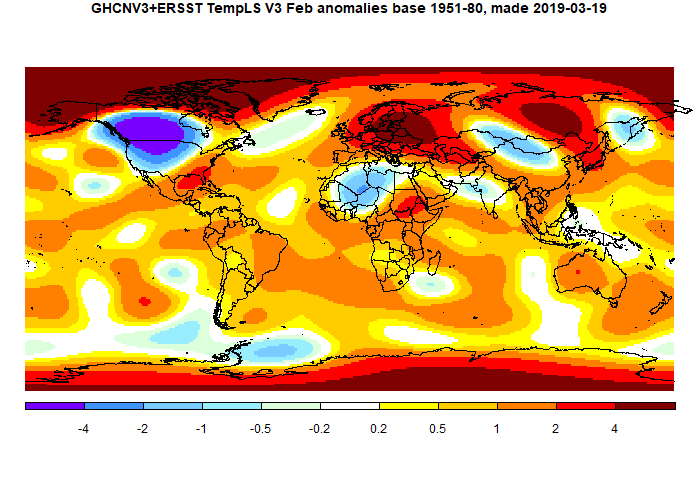
As said above, I'll also show the corresponding V4 plots (GISS is marked beta):
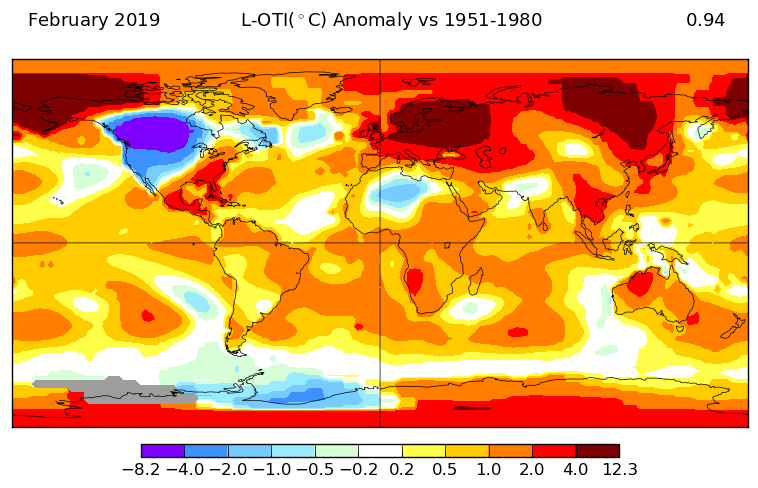
It is similar to V3, but with less grey. Here is the TempLS V4 version, again similar to V3
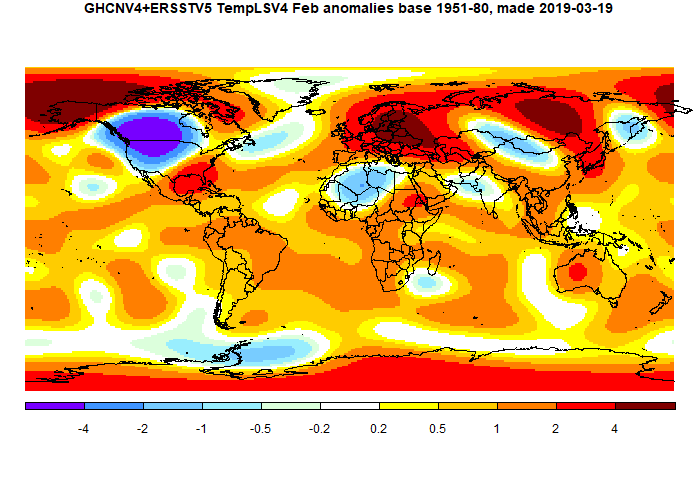
This post is part of a series that has now run for six years. The GISS data completes the month cycle, and is compared with the TempLS result and map. GISS lists its reports here, and I post the monthly averages here.
The TempLS mesh data is reported here, and the recent history of monthly readings is here. Unadjusted GHCN is normally used, but if you click the TempLS button there, it will show data with adjusted, and also with different integration methods. There is an interactive graph using 1981-2010 base period here which you can use to show different periods, or compare with other indices. There is a general guide to TempLS here.
The reporting cycle starts with a report of the daily reanalysis index on about the 4th of the month. The next post is this, the TempLS report, usually about the 8th. Then when the GISS result comes out, usually about the 15th, I discuss it and compare with TempLS. The TempLS graph uses a spherical harmonics to the TempLS mesh residuals; the residuals are displayed more directly using a triangular grid in a better resolved WebGL plot here.
A list of earlier monthly reports of each series in date order is here:
The TempLS mesh data is reported here, and the recent history of monthly readings is here. Unadjusted GHCN is normally used, but if you click the TempLS button there, it will show data with adjusted, and also with different integration methods. There is an interactive graph using 1981-2010 base period here which you can use to show different periods, or compare with other indices. There is a general guide to TempLS here.
The reporting cycle starts with a report of the daily reanalysis index on about the 4th of the month. The next post is this, the TempLS report, usually about the 8th. Then when the GISS result comes out, usually about the 15th, I discuss it and compare with TempLS. The TempLS graph uses a spherical harmonics to the TempLS mesh residuals; the residuals are displayed more directly using a triangular grid in a better resolved WebGL plot here.
A list of earlier monthly reports of each series in date order is here:












OT Nick but I would ask you to consider removing the blogroll link to Watts Up With That. I'm sure you've considered it, but that little nest of deluded vipers is really going beyond the pale.
ReplyDeleteTony,
DeleteI took the view from the beginning that the blogroll was for convenience - ie I put sites there that people might, for whatever reason, want to access. It is not a commendation. And since I fairly often criticised something at WUWT, it seemed logical to provide a link.
But I have to agree that it is particularly bad at the moment, and there is getting to be less and less to comment on there. The day may come...
Fair enough. It is interesting to go back to the early years and see the change in content and comment since. Not that is was ever anything much more than a denier lighting rod. Now it seems desperate to be seen as some kind of political player, like the Fox news of denier blogs or as I like to call it Litebart.
ReplyDeleteMy third or fourth sock-puppet, Kym Smart, is gone, might be my last.
Tony,
DeleteNo need for a sock puppet at WUWT. Nick posts there often, as do I, and no one has ever been banned for civil discourse. It is the most-viewed climate website going, and encourages all viewpoints, as Nick knows well.
Why don't you drop the "den of vipers" attitude, come as yourself and offer your viewpoints in a calm, scientific manner?
James
Tony McLeod. Do you really think you can tell a blog host to remove a link to a website you don't like? Sounds like Twitter behavior, where one can block people who ask uncomfortable questions.
Delete" tell a blog host to remove"
DeleteTony made a suggestion. That is always welcome. As said, I regard the blogroll as a reader utility rather than a list of heroes, so what readers think is important. If people aren't using a link in the roll, I'll take it out. That may happen some day with WUWT, but not yet, I think.
I don't think the viability of WUWT will depend on it!
Nick is only barely tolerated because of his super-human patience and courtesy and even he has been sin-binned. I posted there under my own name for ages but was banned, unfairly IMO. Sock-puppeting was the only way for me to counter some of the lies I couldn't let go unchallenged.
ReplyDeleteSeems to me to be steadily descending into a political echo-chamber, where AGW is a green/communist hoax, so I probably won't bother again. It might have once been loosely described as a "climate website", but those days are long gone and the steam-roller of AGW reality is about to consign it to the dustbin - where it belongs.
Nick, I visit WUWT regularly and I don't agree with a lot of the content, but I do sometimes learn new things there. I always check for any comments you make on interesting posts there and I appreciate those comments. I try to keep and open mind and evaluate as much evidence as possible. That's one of the reasons I come here too. No one has a monopoly on the truth and climate is very complicated. There is always more to learn.
ReplyDeleteThanks, Bryan.
DeleteI like learning too, and there have been times when there were informative articles at WUWT. And if the information was patchy, one could argue. But there isn't much at the moment.
Can I just add my agreement to those above.
DeleteWUWT has always been a hostile environment for those not of the "denier" perspective.
I try to limit my comments to the bits I have expertise in (Meteorology) but have at times complained about Ad Homs there, and a recent one concerning MarkW illicited a personal email from Charles. He assured me there were (big) changes on the way and asked if I would contribute an article. I declined saying that I couldn't stomach the idiots.
Actually, to my eyes the place has become even more of a vehicle for right wing denier rants (Worrell and Ball in particular).
So it chooses it's demographic right there.
Can I also say that I always look for Nick's contributions .... in fact it's the only way I can stay sane in viewing the place - to look out for posts from the (very few) of the knowledgeable (Leif, Nick).
I also learn from the place - but with me v rarely from lead posts. I learn by studying the subject properly before committing it to a post.
After a decade or so of "Climateball" there, of the whack-a-mole myths and rabid conspiracy idiots, it makes you realise that they're not going away, and WUWT will be there long after the "Flying saucer has landed on the White House lawn" so to speak.
I agree that WUWT has had less new evidential information lately. But then as I learn more and more, maybe there is not as much left to learn? The repetition works better for new comers. Unfortunately, WUWT can be a hostile environment for adversarial positions and at times the mud slinging can get nasty, probably a carry-over from the intense politicization of climate science in recent decades. That's one thing I really admire about Nick: he always takes the moral high ground and has the patience to let the Ad Homs slide by to the detriment of those who attack. It actually makes them look bad if that is all they have for rebuttal.
DeleteI never have liked politics, but it seems unavoidable these days. Being a "luke warmer", I tend to disagree with extreme positions on either side of climate science. And being a long time scientist/engineer (40+ years), I know that critical review (healthy skepticism) does have a very necessary and important role in science. So when people broadly say "the science is settled" that's a red flag for me and indicates they are pushing a political agenda (more akin to religion) and not true rigorous science.
I just wish people would be more respectful of others who don't share the exact same opinion on a particular point or topic. My views have changed too many times over the years for me to believe that I am always correct. And too many times I have found that what I thought was true was not supported by a full review of the evidence or by new evidence that was not previously available. Unfortunately, sometimes we never have enough good evidence and what evidence we do have is conflicting and/or confounded by other influences, as seems to be the case in many fields of science, including climate science, health science, and political science among others.
Bryan,
ReplyDeleteI visit WUWT regularly, and I am troubled by some of the ad homs there as well. I'm glad Nick, and also Stephen Mosher, from BEST, do pay visits from time to time. I would really miss them if they quit stopping by, so I hope they can keep hanging in there.
That being said, I do disagree with Nick on the ability to wring any more precision from the data. My degree is in Geology, which required multiple classes in physics, chemistry, geophysics, statistics, calculus -- a very multidisciplinary degree course. In every course that involved physical measurements, the need to properly account for significant digits and uncertainty was paramount. I feel that the climate science field in general does not do a very good job of maintaining this discipline.
In the case of temperature measurements, one has to go back to the very beginning: the daily records taken in thousands of weather stations all over the world. NOAA reports those measurements in tenths of a degree. Those measurements right there forever limit the accuracy and precision that can be attained in calculations down the road, all the way to the global average temperature anomaly.
The limiting factors are the rules of significant digits and error propagation. The most basic rule is that the result from a calculation can be no more precise, and have no more significant digits, than that of the least precise measurement. in this case that would be a temperature measurement in the general form of 12.3±0.05°C. That means the most accurate result of an averaging, or a least squares calculation can go no further than one decimal point in the tenths place, with the uncertainty expressed in the hundredths.
Nick disagrees with me, and has told me he's not working with temperature measurements from weather stations, but with a global temperature anomaly. However, the data that is downloaded from NOAA are the monthly average temperatures, derived from daily weather station reports every five minutes. NOAA ships that data with two places in the decimal, which is over-precise as well. (These rules are not opinions on my part; they are as much a part of physical science as are the laws of gravity and electromagnetism.)
What this means in a practical sense is that statements like "GISS February global up 0.05°C from January, third warmest February," are not supported by the data. The anomaly cannot be stated to that precision, and it falls well within the standard error for a global anomaly.
Climate science is not served by overprecise statements of results.
(Here are a few links to various university physics and chemistry departments that have web pages devoted to the topic of significant digits and uncertainty propagation.)
https://faraday.physics.utoronto.ca/PVB/Harrison/ErrorAnalysis/index.html
http://chemistry.bd.psu.edu/jircitano/sigfigs.html
https://www2.southeastern.edu/Academics/Faculty/rallain/plab194/error.html
James
Actually, this proposition can be tested: take climate model data, which is known to many digits, create an artificial set of weather stations in the model, add some noise to each weather station, then round the data for each weather station to the tens digit, and then perform an anomaly calculation. The anomaly calculation can be compared to the answer depending on stations without rounding, then without noise, and then the actual calculated anomaly for 100% coverage. I believe this has been done (including by Nick), and it has been shown that in fact you can take a few hundred weather stations, add noise, round off, and still get a very accurate emulation of actual anomaly changes.
Delete-MMM
"and it has been shown that in fact you can take a few hundred weather stations, add noise, round off, and still get a very accurate emulation of actual anomaly changes"
DeleteIndeed so. I did it here, for example. I took 12 months of Melbourne's daily maxima, reported to 0.1°C, and calculated the monthly averages. Then I rounded the original data to the nearest degree, and repeated the calculation. The revised calc agreed within about 0.05°C, not 1°C. That is pretty close to the theoretical value.
JamesS, I've had a strong interest in geology since I was a child, but ended up pursuing meteorology in college, which led me into environmental engineering and air quality meteorology. In addition to meteorology, rigorous climate science must also incorporate many aspects of geology, geography, oceanography, and even astronomy (solar output and earth's orbital/rotational mechanics) to be successful, especially for longer term analyses and forecasts/projections on the order of decades to centuries to millennia and beyond.
DeleteI wish we had modern observations similar to those from the last 40 years to cover the last few tens of thousands of years or more. Without them, there is much more uncertainty in estimating past regional and global climates. And that uncertainty increases as you go back in time beyond 40 years. Even with our modern measurements, I see some limitations to accuracy that have not been well characterized by most assessments I have seen.
Most of the global temperature anomaly assessments I have seen appear to be characterizing precision more than accuracy. Better characterization of accuracy may require hundreds of years of modern observations before we can get a good assessment of accuracy. I posted some thoughts about accuracy related issues four years ago here (although it is certainly not comprehensive and is quite subjective).
I prefer seeing temperature output at greater resolution than may be justified by our present best understanding of precision or accuracy. So, I have no problem with seeing global temperature anomalies presented to three decimal places. Some patterns may be resolved well with current precision, even though they could be offset (biased) in accuracy. The patterns may still provide information even though we cannot "calibrate" them to better accuracy.
James,
DeleteA thing I complain of in this sig fig stuff is that people won't properly cite authority, or even explain clearly what the rules are supposed to be. They cite links, but not what it is in them that supports their case. I looked up the first of your links
https://faraday.physics.utoronto.ca/PVB/Harrison/ErrorAnalysis/index.html
It's just orthodox statistics. They have a section on Error in the Mean. It just says what we have been saying:
"The fact that the error in the estimated mean goes down as we repeat the measurements is exactly what should happen. If the error did not go down as N increases there is no point in repeating the measurements at all since we are not learning anything about Xest, i.e. we are not reducing its error."
"If you repeat a measurement 4 times, you reduce the error by a factor of two. Repeating the measurement 9 times reduces the error by a factor of three. To reduce the error by a factor of four you would have to repeat the measurement 16 times."
Apologies Nick for OTing the comments. While quite a bit of the more technical statistics you discuss goes over my head I'm highly appreciative of the time and effort you commit to document GW.
ReplyDeleteThanks, Tony. No problem about the OT - there wasn't any pressing alternative discussion to be derailed.
DeleteJames
ReplyDeleteI’ve never had a stats class, but here’s an idea - let’s look at some random temperatures, and then round to the nearest 10th:
12.28 = 12.3
14.22 = 14.2
9.79 = 9.8
11.21 = 11.2
15.26 = 15.3
14.37 = 14.4
10.82 = 10.8
13.66 = 13.7
7.94 = 7.9
Calculating the average for each column:
12.17222 / 12.17777
The two values are only .00555 apart. I’m guessing the more temperatures we look at, the closer the two averages will get.
Snape,
DeleteGood idea. Let's take the 30 years of, say, March temperatures from 1951-1980 that's used for creating the baselines for determining the anomaly. I'll use the data from the Canberra Forestry site. I don't know what that is, but it has a nice sound.
20.00 = 20.0
18.61 = 18.6
18.23 = 18.2
16.84 = 16.8
18.11 = 18.1
18.18 = 18.2
17.40 = 17.4
17.89 = 17.9
18.19 = 18.2
17.98 = 18.0
17.13 = 17.1
18.01 = 18.0
18.17 = 18.2
17.91 = 17.9
18.48 = 18.5
17.42 = 17.4
16.96 = 17.0
20.51 = 20.5
18.54 = 18.5
16.27 = 16.3
18.62 = 18.6
17.42 = 17.4
17.78 = 17.8
18.85 = 18.9
16.67 = 16.7
18.34 = 18.3
17.82 = 17.8
19.09 = 19.1
18.63 = 18.6
19.87 = 19.9
18.130666666666700 = 18.130666666666700
18.13 = 18.1 Mean
0.94 = 0.9 Standard Deviation
0.17 = 0.2 Error in the Mean
You can see that you're correct. With 30 samples, and the mean calculated out to 15 places, there's no difference. So what's the difference?
The difference is in how experimental measurements are calculated and reported. Ask yourself the question: if we've only measured the temperature to the tenths of a degree, how can we claim to know the mean to 15 places? We can't. We can only report that which we do know.
I've added in to the calculations the standard deviation and the error in the mean, two figures that are very important in reporting the results of a calculation involving physical measurements such as temperatures.
The standard deviation (s) of a set of numbers (a population) is the average of the distance of each individual measurement from the mean. You calculate the mean, you subtract that from each measurement, and average those distances to get the SD. It's a measure of the spread of the data relative to the mean.
The Error in the Mean (SE), is the standard deviation divided by the square root of the number of measurements; in this case, the square root of 30. This number means that with the same number of repetitions, the average value from the new experiment will be less than one standard error away from the average value from this experiment.
Respecting those rules is paramount. The GISS report is based on the same data Nick uses. The daily station data is in tenths of a degree, the monthly summary is in hundreds of a degree. This is over precise, because the calculation from data cannot be more precise than the least precise measurement in the calculation. The correct value is 19.9±0.2°C
To get a global anomaly, calculations are done to weight the monthly data by area, so that areas with lots of stations don't overpower areas with just a few stations. But those calculations can't report a more precise result that those original weather stations: to one tenth of a degree, plus or minus the standard error.
The Standard Error is the only part of the result that can be reduced by using a large population. This is limited, though, by the fact that the square root of the population is divided into the standard deviation to get the uncertainty.
The endpoints of the GISS map are at -8.1 and +12.3, which roughly correcponds to a standard deviation of 3.2, assuming a near-normal distribution. We can test scenarios to see how the standard error is changed by station population.
SE = 3.2/sqrt(5000) = 0.045
SE = 3.2/sqrt(10000) = 0.032
The uncertainty in the mean with 10000 station reporting is nearly the same as the GISS anomaly change, and as I see it, that's a problem. That increase is statistically insignificant. It's beyond the level of precision that can scientifically be reported from the starting data, and the amount of the rise is practically the same as the uncertainty in the mean.
A proper reporting would be the anomaly is unchanged for February, for whatever warmest February that would make it.
Believe it or not, a large part of the skeptic response to anomaly reporting is based on this type of over precision. If the reporting held more closely to the scientific rules, that angle of disagreement would be removed.
James,
Delete"Ask yourself the question: if we've only measured the temperature to the tenths of a degree, how can we claim to know the mean to 15 places?"
They are different things, so why not? (15 is an exaggeration, of course). But the better knowledge of the mean is common understanding. Why do hard-headed commercial people, eg drug companies, go to expense to gather large samples to average? Because the averages thus gained are a more accurate measure of the population mean that they are seeking.
"Respecting those rules is paramount."
You're saying many of the right things, and even doing the right arithmetic. Yes, the standard error of the mean is reduced - by 1/sqrt(N) if the rv's are independent, etc. That is what it says, the uncertainty of the mean. It is different, and less than, the uncertainty of individual measurements.
In fact, the uncertainty of GAT derives not from the uncertainty of individual measurements, which contributes little, but to uncertainty about how representative they are - ie whether looking in different places might give a different answer. That is what you really need to watch, and what I spend a lot of time on.
James
DeleteI’ve done a little reading and am confused by this:
“0.17 = 0.2 Error in the Mean”
If the 30 measurements you provided are considered a population, then the mean of that population is 18.130666666666700
This, it seems to me, is not an estimate and therefore doesn’t need a measure of error attached. The only error would be human, i.e. entering a wrong digit into your calculator.
On the other hand, if we took a random sample of that population (let’s say 5 individual measurements) and calculated the mean, the result would likely differ from the mean of the total population (parametric). The sample mean could only be considered an estimate. Isn’t this the sort of situation where you would want to determine a standard margin of error? In other words, “how much does the sample mean tend to differ from the parametric?”
Okay, James, here is an experiment you can do at home:
DeleteTake Excel. In column A, use the equation RAND()*10. Now copy that down for several hundred cells. Copy this column using "paste values" to column C in order to freeze the data. Column C represents the "true historical data".
In column D, add 0.01 to Column C. This is the "true present-day data" after a warming of 1 hundredth of one degree.
In column F, use the equation ROUND(C,1). This is now the observed historical data, with a precision of a tenth of a degree. Do the same in column G for the present-day data.
In column J, put in the equation AVERAGE(G$1:G2)-AVERAGE(F$1:F2). Copy that down the column. This is the estimated warming based on the observed data.
Now, the real increase in temperature was 0.01 degrees, but the observations have a precision of only 0.1 degrees. And yet, magically, we can get to pretty close - within 50% - to properly estimating the 0.01 temperature change using the observations within a few dozen samples!
(you can repeat this again where you add noise of size 0.1 using RAND()*0.1 to both the historical and present true values before rounding... then it still takes less than a hundred observations to stabilize within 50 percent of the right answer, even though the signal is one tenth the size of BOTH the rounding AND the added noise).
Does this help at all with your comfort regarding the reporting of global anomalies?
-MMM
Nick,
DeleteJames: how can we claim to know the mean to 15 places?"
Nick: They are different things, so why not? (15 is an exaggeration, of course).
It's because you have to deal with the significant digits in the original measurements, and the result can't have more than the data with the least. The web page of the chemistry department at Penn State puts it this way as part of a question/answer segment. I've trimmed for length, but left in teh important points.
Example #2: How many significant figures will the answer to 3.10 x 4.520 have? [the calculator answer is 14.012]
Three is the correct answer. 14.0 has three significant figures. Note that the zero in the tenth's place is considered significant. All trailing zeros in the decimal portion are considered significant.
Sometimes student (sic) will answer this with five. Most likely you responded with this answer because it says 14.012 on your calculator. This answer would have been correct in your math class because mathematics does not have the significant figure concept.
The last sentence describes the difference between taking physical measurements and doing math. Significant digits must be considered when giving results of physical measurements. An anomaly is given in units of °C, so it's a physical measurement.
Nick: ...the uncertainty of the mean. It is different, and less than, the uncertainty of individual measurements.
I agree. But it's the uncertainty in the mean, not the precision. You can't add significant digits to the result to match the uncertainty. I think you mentioned in a earlier post that when you checked TempLS3 with a pure monthly average - baseline average, the error in the mean was usually around 0.02°C. That's the same ballpark I get, but that doesn't mean the anomaly precision goes to the hundredths place as well. It would be stated as something like 0.6±0.05°C.
That might be done with pure statistics, but when working with physical measurements the "sigdigs" have to be accounted for.
Snape,
Delete"If the 30 measurements you provided are considered a population, then the mean of that population is 18.130666666666700
"This, it seems to me, is not an estimate and therefore doesn’t need a measure of error attached. The only error would be human, i.e. entering a wrong digit into your calculator."
The Penn State chemistry department web page puts it this way:
"Exact numbers, such as the number of people in a room, have an infinite number of significant figures. Exact numbers are counting up how many of something are present, they are not measurements made with instruments."
In this case, we are dealing with measurements: the temperature, in °C., so the "exact number" scenario isn't in play. A standard deviation of 1.5C means that if you take another measurement, you can be about 68% sure that the measurement will be within 1.5C of the mean. The error in the mean says that if you repeat the entire measuring process over again, with new readings, the average from that exercise will be within one standard error (the error in the mean) of the original mean.
Snape: if we took a random sample of that population (let’s say 5 individual measurements) and calculated the mean, the result would likely differ from the mean of the total population (parametric). The sample mean could only be considered an estimate.
I agree. And that's where we are with the average global anomaly. We can't possibly sample the entire Earth's surface, so we take what we get, average them, homogenize them across weighted areas , and get an estimate. We can't even truly repeat the experiment, because temperatures change constantly, and the highs and lows at each station will be different tomorrow. Since we know we're taking a random sample, and we know we're only calculating an estimate, we have to maintain significant digits and uncertainty appropriately.
OK, James, if you want to follow those rules, which aren't very useful here, then let's do it. Suppose you have 100 numbers, all about 50, and known to nearest integer. 2 sig fig. But the total is about 5000, still, as your rules would have it, known to nearest integer. You don't lose dp by ading. But now you have 4 sig fig. Divide by the total, which as your rule says, has infinite precision. Then the answer is still known to 4 sig fig, and is about 50. So you would be allowed 2 dp, under the rules.
DeleteStats would say the uncertainty is about 0.1.
Anonymous:
DeleteThere are a few things wrong with your scenario. The first, and major, problem is that Excel is storing the values to the extent of its abilities; the rounding is done just for display. When the averaging happens in column J, Excel is doing the full-digit calculation. The result isn't rounded to one decimal point, either. If that is done, all of column J becomes 0.0.
Secondly, a measurement of 0.01 increase from one day to another is outside the measuring ability of the thermometer. NOAA lists the daily measurements in tenths of a degree, with a probable measurement error of ±0.05°C. A 0.01C change wouldn't be noticeable.
Third, the standard error (error in the mean) of the two data columns is ±0.1C. A 0.01C change falls within the range of uncertainty, meaning that the value is statistically insignificant.
Nick discounts the daily measurement error, and I agree, because it more or less disappears when the monthly and annual rollups occur. What's more important by far is the standard deviation s and standard error (error in the mean) SE of the monthly and annual averages.
James: Look up the ROUND() function in Excel. It actually rounds, such that the value in the cell only stores 1 digit past the decimal.
DeleteSo really. Try my exercise. You'll see that even in a case where the measurement is a tenth of a degree, with an error of a tenth of a degree on top of that, you can detect a change of one hundredth of a degree with a hundred or so measurements.
Stop relying on this one heuristic you think you know (e.g., that you can't know an average with more precision than the uncertainty in your measurements) and actually test it with an artificial situation where you know the real answer to many significant figures, and you can see if you can estimate that answer using rounded numbers. And the answer is that YOU CAN. Then, you can go back and try to understand why your heuristic is wrong in this case.
-MMM
Nick,
DeleteThe problem with the 100 numbers, all around 50, is that the result has to use the least number of significant digits of the values, not the most. The Penn State chemistry department puts it like this:
"In mathematical operations involving significant figures, the answer is reported in such a way that it reflects the reliability of the least precise operation. An answer is no more precise that the least precise number used to get the answer. Your answer cannot be MORE precise than the least precise measurement. "
It would also matter what the total was. If it were exactly 5000, that's only one sig fig. On the left side of the decimal, only zeroes between non-zero digits count as sig figs.
The chem website sums it up this way:
"in science, all numbers are based upon measurements. Since all measurements are uncertain, we must only use those numbers that are meaningful."
There's a difference in statistics between whole, exact numbers like the count of people in a room, or votes on a poll. Of course, a random sample like a poll has its uncertainties, as we see when they the results are given with "+3/-4 points", or words to that effect.
Nick, you've been very kind to suffer my goings-on about this. I won't take up any more of your time and space here. I do have a Wordpress site where this conversation can carry on, if anyone's interested. If anyone is, let me know and I'll set up a page.
Thanks!
Anonymous,
DeleteYou're missing my point. Obviously a calculator can report any number of places in an answer. The point is -- and this is not an opinion of mine, but a rule of scientific calculation -- regarding scientific measurements, the answer may only be as precise as the least precise measurement.
Obviously, the temperature is constantly changing, from second to second. A standard thermometer just as obviously can't capture those microchanges, which is essentially what you're proposing. When NOAA reports the daily temps, they do in tenths of a degree. They give the monthly summaries to hundredths of degrees, which is overprecise.
Like I said before, the problem in my view is that the values reported are just a bit over precise. I don't think the starting data justifies three-decimal point precision. I think saying an anomaly is up 0.033 is statistically insignificant. I think a lot of the skeptical community would be less skeptical if a decimal point (or in some cases, two) were trimmed from the results reporting.
James: the problem is that you just keep repeating "the answer may only be as precise as the least precise measurement" without understanding that it is a short-hand heuristic. Sig-figs are an approximation to rigorous uncertainty analysis.
DeleteWhat my example (which you clearly haven't attempted) demonstrates is that there is a signal of magnitude 0.01 that CAN be reliably detected even though the measurements are rounded to 0.l (and, as a additional test, even when I add additional noise of magnitude 0.1 to all measurements before rounding).
Some citations critical of blind reliance on sig figs:
https://www.av8n.com/physics/uncertainty.htm#sec-execsum-sigfig
https://acarter.people.amherst.edu/documents/tpt2013.pdf
-MMM
Anonymous,
DeleteI promised Nick I wouldn't take up more of his blog with this discussion, but I would love to continue it. I've set up a page on my Wordpress site where we can carry on if you'd like to. I've not much experience in working with Wordpress, so bear with me if you decide to come over and there are any technical issues.
The page is
https://jaschrumpf.wordpress.com/2019/03/28/talking-about-temperatures/
I did perform your experiment, and I have read the articles you linked to. So come on over if you like, and we'll continue. Everyone is welcome, if they're interested.
Thanks. I've enjoyed the discussion.
Nick
ReplyDeleteMaybe you could delete all but my first comment? Also, sorry about the inappropriate attempt at comedy last month. I very much admire and appreciate the work you do.
Thanks, and done. But you should be able to delete them yourself, with the delete button next to reply.
DeleteThanks, Nick
ReplyDeleteI don’t see a delete option, but I think the problem is on my end.
Nick and Snape, I don't see a delete option either and I tried two different browsers, Firefox with NoScript and Opera.
DeleteYes, it seems to be patchy. But some commenters have been able to delete their comments. Blogger gives extra privileges to people who log in with a Google Id, and maybe some others.
DeleteWell, oddly I'm seeing the delete option now. I guess it must be a bit patchy.
DeleteAll I know is the March GISS anomaly is going be a whole bunch.275639251899 bigger than the February GISS anomaly was.
ReplyDeleteThe 2 meter anomaly at Climate Reanalyzer has been similar to October, 2017. UAH was 0.63 C that month.
ReplyDeleteAlso, another “heat wave” in the Bering Strait area.
https://climatereanalyzer.org/wx/fcst/#gfs.arc-lea.t2anom
The October 2017 spike was mainly in the upper air, not so much at the surface. However, March 2019 is quite near the the temperatures of February- March 2017, which probably was the warmest period on record, adjusted for ENSO (e g look at Nick's NCEP/NCAR)
DeleteThe daily CFSR/CDAS global surface temperature estimate (for air 2 meters above ground level) just spiked up to 0.872C for 2019 March 29, which is the highest since 0.909C on 2017 March 29 (referenced to 1979-2000). That is an increase of 0.874C since the low of -0.002C on 2019 August 26, which was the lowest since -0.010C for 2014 June 30. Wacky weather to say the least.
ReplyDeleteThe latest peak was driven primarily by the very high Arctic temperature anomaly of 6.274C for 2019 March 29, which is the highest since 6.350C on 2016 November 21. Graphs here.
Looks like the March 2019 CFSR/CDAS GMSTA will be about 0.24C higher than February and will be the third highest March GMSTA since 1979, behind 2016 and 2017 (but only about 0.01C below 2017).
Also of interest, the running 365-day CFSR/CDAS GMSTA has increased about 0.02C over the last month. That's after a two year fairly steady downward drop of about 0.23C.
Thanks, Bryan,
DeleteThat is a useful collection f graphs.