Inevitably, the first comments are along the lines of "can't be acidification until pH7" (never with a reference). I blogged on that here. I'd like to take up two points from that - Lewis acidity and buffers. The general aim of this post is to put pH in context. It's over-used.
Lewis Acid
Early definitions of acidity relied on the properties of hydrogen ions, and of course pH is central. But in 1923, Lewis generalised the notion of acidity to the sharing of electron pairs, which needn't involve hydrogen.That's an important simplification. In fact, H+ has very little final role in the seawater reactions. You can express them as:
CO2 + CO3-- + H2O ⇌ 2HCO3-
Ca++ + CO3-- ⇌ CaCO3
No protons, but the Lewis acid CO2 reacts with the base CO3--, shifting the solubility equilibrium.
Buffers
Buffering is often thought of as pH buffering, but again I'll aim to generalise. In fact, it's just a consequence of ternary equilibrium:H + A ⇌ HA
The Law of Mass Action gives the equilibrium relation:
[H][A]/[HA] = K
If K is of moderate size, and [H] is small relative to [A] and [HA], then whether the reaction moves back or forward, [H] remains relatively fixed because the dominant species don't change much in proportion.
The familiar pH version arises when HA is a weak acid and [A] a weak base. Then [H+] is small, and relatively fixed (buffered) by the equilibrium.
A common sceptic scoff at acidification is, how could so few H+ ions make a difference? At one level it's right - they can't directly. But what buffering means is that if [H+] changes, then something else has changed, by a lot. And that is what is likely to cause changes.
Sea-water reactions
These were listed above:CO2 + CO3-- + H2O ⇌ 2HCO3-
Ca++ + CO3-- ⇌ CaCO3(aragonite)
I'll ignore the effects of hydration of both H+ and CO2
There is an excellent review article by Zeebe which sets this out in much more detail, and I'll refer to it later.
The effect is that when CO2 is added, the first equilibrium shifts to the right, CO3-- is diminished, shifting the second equilibrium to the left. The equations can be combined:
CO2 + CaCO3 + H2O ⇌ 2HCO3- + Ca++
This emphasises that ultimately each extra molecule of CO2 tends to dissolve a molecule of CaCO3, if equilibrium shifts to the right.
pH Equilibrium relations
The equilibria can also be expressed as the more traditional diprotic acid-base expressionsCO2 + H2O ⇌ HCO3-+ + H+; pKa=5.94
HCO3- ⇌ CO3--+ + H+: pKa=9.13
The pKa values are the log10 of the equilibrium constants.
The equilibrium can be shown against pH as Bjerrum plot. This shows relative concentrations normalised against DIC = dissolved inorganic carbon. This is just the sum:
DIC=[CO2]+[HCO3-]+[CO3--] Here is the plot:
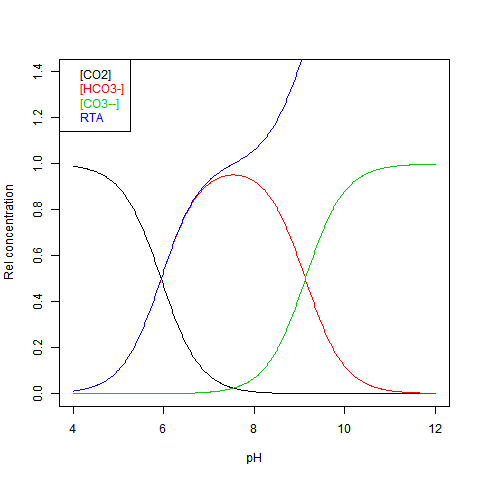
RTA stands for Relative (to DIC) Total Alkalinity - see next.
Equilibrium relations - some numbers
I'm following the Zeebe review article here. Typical values for dissolved species:- DIC 2.05E-3 M (M = 1 mol/l ~ mol/kg)
- Total Alkalinity=[HCO3-]+2*[CO3--] = 2.35E-3 M
- ratio %: [CO2]:[HCO3-]"[CO3--]=0.5:89:10.5 at pH 8.2
- So [CO2]=1E-5 M, [HCO3-]=1.82E-3 M, [CO3--]=2.1E-4 M
- At pH 8,2, [H+]=6.3E-9 M; [OH-]=1.6E-6 M;
Sea Water measurement
Eli had a post arising from these threads on pH measurement. It's hard. However, there is a new method, probably less accurate, but suitable for continuous monitoring. It uses an ion-selective field FET, SeaFET, which can be set in place for months at a time. But, as insisted here, pH is over-emphasised. It follows the major species, and they can be used to measure it. Two quantities easily measured by flask analysis are all you need. One is DIC. This can be measured gravimetrically. The other is Total Alkalinity (TA) TA=HCO3-]+2*[CO3--] This can be determined by acid titration with an indicator that changes about pH=4.5, which removes almost all bicarb and carb. The titration also picks up borate and hydroxide, and [H+] needs to be subtracted, but these are small effects which I will ignore here. All you need are the values of DIC and TA - both easily obtained by flask analysis. The point is they are present in much larger concentrations, and are more stable.Use of equilibrium relations
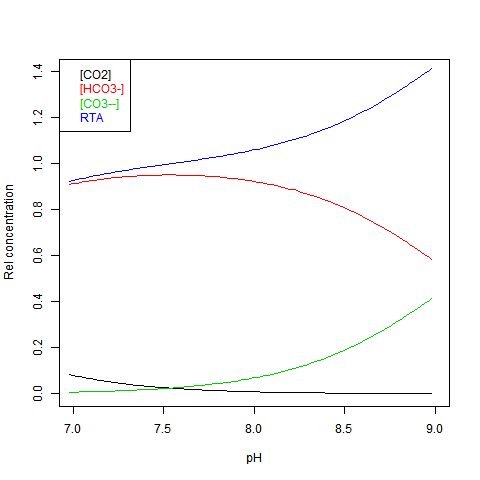
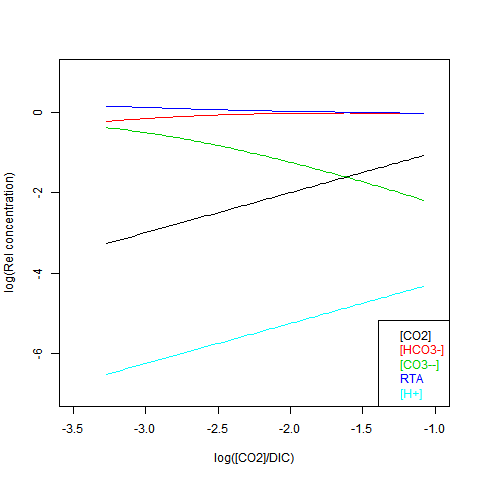
Given DIC for normalisation and any other concentration (in particular TA), you can read a pH value from the Bjerrum plot, and deduce everything else. But here are some more convenient log plots. Firstly with pH again on the x-axis, but log10 on the y-axis. Note that both log([CO3--]) and log([CO2]) vary close to linearly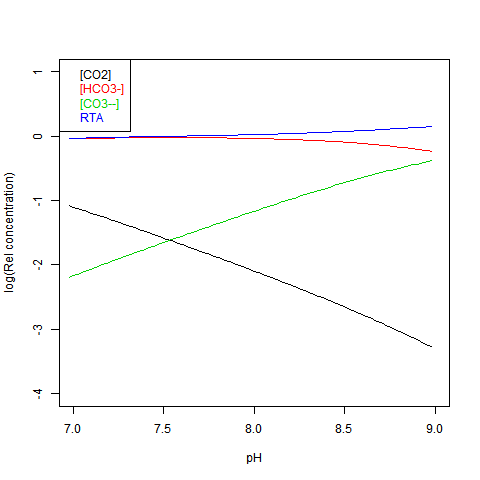
Now shifting the relative total alkalinity RTA to the x-axis. This allows the other values to be read explicitly:
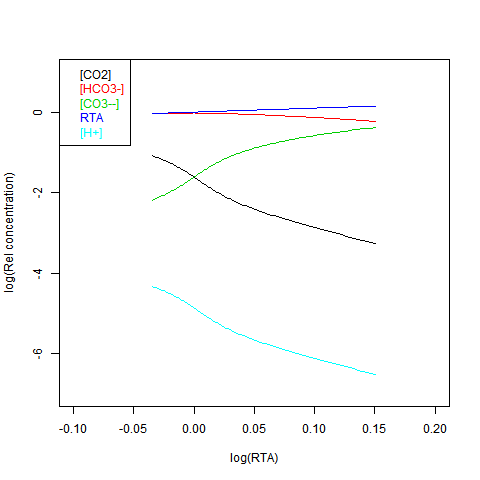
RTA is easily obtained, but doesn't preserve the linear relations. Here is log([CO2]) on the x-axis:
Solubility equilibrium
The end problem is dissolution of CaCO3 structures. Two reasons are sometimes given why this may not matter
Biological deposition is complex - not just a solubility product
- The oceans are supersaturated relative to aragonite formation (the CaCO3 form used by most organisms).
Discussion
What I hope these plots will show is that pH is just one of a number of co-varying quantities, and because of the small number of ions represented, is far from the most important. You can use it to track the reaction if convenient, but you don't have to. It's an intermediate - the nett reaction is CO2 neutralising CO3--, producing HCO3-. This then affects the CaCO3 solubility equilibrium. The secondary role of pH is relevant to the following things that have been said in the acidification discussions:- "Acidification requires pH<7
pH is just an indicator of the carbonates equilibrium. pH 7 has no relevance.
- The number of H+, even with acidification, is too small to matter
True, H+ are not the problem
- pH measurements are sparse and inaccurate
But not TA/DIC, which is enough.












I disagree with your first statement. Proton transfer is very much involved in the CO2/HCO3-/CO3^2- equilibrium, which is in the Bronsted/Lowry framework is written as::
ReplyDeleteCO2 + 2 H2O <-> HCO3- + H3O+
HCO3- + H2O -> CO3^2- + H3O+
The second reaction is a conventional Bronsted/Lowry proton transfer, with a Ka (acid dissociation constant) that you can look up in a textbook. The first is more complicated since it involves coupling between the dissolution of carbon dioxide and reaction of the dissolved carbon dioxide with water, but still fits into the proton transfer framework. Adding these together to give an overall net reaction between CO2 and CO3^2- , as you do in your first equation, is convenient for accounting purposes but obscures what is going on at the molecular level, which is proton transfer between water and the carbonate and bicarbonate ions.
This doesn't affect the remainder of your post.
Robert
Robert,
DeleteI said "In fact, H+ has very little final role..."
I agree it is involved in the mechanism - there would be a number of intermediates. But the H+ is created by the first reaction and destroyed by the (back) second reaction, so its concentration is controlled by the respective equilibria.
I used the pKa (per Zeebe) values to generate the plots.
I find this a bit odd. According to this reaction mechanism protons do not play a role in the solubility of CaCO3. How then do you explain the solubility of CaCO3 in acid solutions, for instance etching of marble by acid?
ReplyDeleteThe dissolution of CaCO3 by acids is not essentially different from that of e.g. calciumphosphate salts. In both cases it is caused by a shift in the equilibrium, due to a pH-dependent decrease in the concentration of one of the reactants, CO3-- or PO4 --- (for that matter). In the CO2-driven dissolution of CO3--, CO2 is the source of both the acid and one of the reactants, which makes it less straight forward. (Btw the same occurs in the dissolution of calciumphosphate by phosphoric acid).
So let's sum up all the reactions involved:
CO2 + H2O <-> H2CO3
H2CO3 <-> H+ + HCO3-
HCO3- <-> CO3-- + H+
Ca++ + CO3-- <-> CaCO3
---------------------- +
CO2 + H2O + Ca++ <-> CaCO3 + 2H+
Adding a strong acid, HCl, will drive the equilibrium to the left--> dissolution of CaCO3.
Adding CO2, will first drive the reaction to the right and the calcium ion solubility will decrease. At increased [CO2](> 10-6 atm) the calcium ion solubility will increase. At pH 7.3 (pCO2 = 0.01 atm) the calculated solubility is approx 1 mM, which is still lower than the calcium ion concentration in seawater (about 10 mM).
"I find this a bit odd. According to this reaction mechanism protons do not play a role in the solubility of CaCO3."
DeleteI'm saying that in seawater, the aprotic Lewis acid CO2 dissolves CaCO3. Protons are involved as intermediates. Sure strong acids will dissolve it too, and protons are involved there. The difference is that there protons are supplied as an abundant species.
I don't agree with your last summed reaction. H+ is not the product - there is never more than a tiny amount in seawater. And CO2 does not produce CaCO3; it dissolves it. That's the point of the buffering argument; only the weakest acid and weakest base can coexist in abundance. H+ as a product would immediately react with CO3--, or even HCO3-.
That's why I think the correct way to combine those reactions is to eliminate H+, H2CO3 and CO3-- to give
CO2 + CaCO3 + H2O <-> Ca++ + 2HCO3-
That's the actual reaction, in karst, for example. You get calcium bicarbonate. It's also the second stage reaction when you blow into limewater.
Any linear combination of equilibrium equations is another equilibrium equation, all of which are equally "correct". I agree that the net equation is the most convenient one to use for calculations, but I reiterate that it obscures what is going on at the molecular level. CO2 does not react with CaCO3, it reacts with water to make HCO3^-. CaCO3 does not react with CO2, it reacts with water to make HCO3^-. In the first reaction, CO2 is the (Lewis) acid and water is the base. In the second, water is the (Bronsted) acid and CO3^2- is the base. We can study each of these reactions independently - by exposing distilled water to air, or by putting limestone into distilled water. Nothing fundamentally changes at the molecular level when we put CO2, water, and CaCO3 together in one beaker (or one ocean) - the equilibrium concentrations adjust, but the underlying mechanisms are the same. CO2 molecules do not swim up to CaCO3 crystals and help them to dissolve; instead, CO2 molecules increase the H^+ concentration in water, which helps the water to dissolve CaCO3 by converting CO3^2- to HCO3^-.
DeleteRobert
Robert,
DeleteI think the use of equilibrium relations is that they do reflect a quantitative outcome. They don't reflect mechanism, but we may not need to know that. If we do, it's probably a lot more complicated than just proton intermediates.
And yes, you can get many "correct" equilibria. But the useful ones are the ones that can move reasonably independently. That's why
CO2 + CaCO3 + H2O <-> Ca++ + 2HCO3-
is useful, because it is indeed possible that added CO2 will lead to a measurable amount of each product, according to the equilibrium stoichiometry. While with
CO2 + H2O + Ca++ <-> CaCO3 + 2H+
the forward reaction can only happen significantly coupled with something else, because [H+} must remain low. And the back reaction can only happen if some coupled reaction is supplying H+.
Nick, I don't think we are far apart. Indeed, this discussion has reminded me of one of the lessons that I try very hard to impress upon students: when analyzing chemical equilibria, start out by identifying the *major species* that are present. Then express your equilibrium equations, as far as possible, in terms of these major species. That is the quickest and most reliable way to get useful quantitative results, even though it may not give us an accurate description of what happens at the molecular level. Understanding chemistry requires learning how to think analyze chemical reactions from multiple perspectives.
DeleteWhat bothered me in your initial post were these two statements:
"In fact, H+ has very little final role in the seawater reactions." and "the Lewis acid CO2 reacts with the base CO3--"
Just because H+ can be cancelled out of the equations does not mean that it does not play an essential role. The H+ ions don't physically disappear when you algebraically eliminate them. And the second statement is just wrong: in the Lewis framework, an acid accepts an electron pair from a base to form an "adduct". CO2 does not accept an electron pair from CO3^2-. CO2 accepts an electron pair from water, and CO3^2- donates an electron pair to water. Each of these reactions can be observed to take place in the absence of the other (by exposing water to air containing carbon dioxide, or by putting limestone in water.)
So I repeat: CO2 does not react with CaCO3, it reacts with water.
CaCO3 does not react with CO2, it reacts with water.
The equations that are most convenient for setting up calculations do not accurately describe what happens at the molecular level.
Robert
Robert,
Delete"So I repeat: CO2 does not react with CaCO3, it reacts with water."
Yes, I agree. I should at least have said "CaCO3 reacts with CO2 and water". But in using the combined equation, I have company. Zeebe uses it too.
But you can't pin these things unambiguously. On the face of it, CaCO3 doesn't react with water - it dissolves. CO3-- reacts with water. etc.
The point I'm trying to convey is the outcome. If you add a mole of CO2 with CaCO3 present, you get the best part of 2 moles HCO3-, a fraction of a mole CO3--, and a very small fraction of a mole CO2 remains. The extra HCO3- comes from both the CO2 added and CaCO3 dissolved, so at equilibrium, a mole of CO2 dissolves nearly a mole of CaCO#. Of course, equilibrium is an elastic term in the heterogeneous ocean - CaCO3 is not always present, so the "equilibrium" is reached only after a long mixing time delay. It is often said that the ocean is supersaturated with CaCO3 - I'd be interested to see how that statement interacts with the heterogeneity.
Nick: Carbon dioxide itself is not a Lewis acid. It reacts with water to make a Bronsted-Lowry (protic) acid, H2CO3. The equilibrium for this reaction lies far on the side of CO2 (the gas, dissolved in water). The equilibrium constant for CO2 + H20 <==> HCO3- + H+ is the product of the equilibrium constants for each step: CO2 + H2O <<==> H2CO3 <==> HCO3- + H+.
DeleteA Lewis acid has an outer shell of electron around one atom which is formally (at least) two electrons short of being full. The boron on B(OH)3 formally has only six electrons, the pair it shares with each oxygen. The outer shell of central carbon in C(=O)2 is complete by sharing four electrons with each oxygen. In both cases the polarity of the oxygen bonds reduces the electron density around the central atom, but Lewis acidity refers to accepting a pair of electrons, not just polarization of bonds within a molecule. LI+ is a Lewis acid; in water it goes around as Li(H20)4+ in order to fill its outer shell. Unlike (H20)B(OH)3, Li(H20)4+ has little tendency to ionize to (HO)Li(H20)3 + H+.
Frank
Frank,
Delete"Nick: Carbon dioxide itself is not a Lewis acid. "
How do you interpret the dry reaction
CaO + CO2 <-> CaCO3 ?
On p 4 here is an interpretation of CO2+H2O<->H2CO3 as a Lewis acid-base reaction.
I agree that here most of the acid-base reactions are protic. But you can still trace through to see what was looking for an electron pair and how that was satisfied, after the intermediates came and went.
Sorry, on p6
DeleteNick: CaO + H2O ==> Ca(OH)2. If you heat CaCO3 (limestone, marble etc.), you can drive off a molecule of CO2, making CaO. I assume this happens underground and is the source of the CO2 that volcanos return to the atmosphere. When the lave is eroded, CaO becomes CaO becomes Ca(OH)2, which then reacts with a molecule of H2CO3 (from CO2 plus water) to make CaCO3 (and two waters). This completes the cycle.
DeleteFrank
Frank,
DeleteI'm asking about the dry reaction. As in a lime kiln. It's a real equilibrium, which determines the operating temperature. And there's no water there.
Nick: I can't claim much experience with solid-phase reaction at high temperature, but the following thoughts seem reasonable. The "dry reaction" obviously could be catalyzed by water. Combustion of wood or non-anthracite coals produce water which could catalyze the reaction. Strongly basic materials like CaO are rarely totally anhydrous; their surface may be coated with a layer of Ca(OH)2. Ca(OH)2 certainly certainly should be able to react with CO2 (in solution or solid-phase); H2CO3 doesn't need to be involved. The principle of microscopic reversibility must apply: If heating anhydrous CaCO3 liberates CO2 and CaO without being catalyzed by water, then CaO can certainly absorb CO2 to make CaCO3 without being catalyzed by water. And I suspect that if you heat completely anhydrous CaCO3 hot enough, it will find some way to lose CO2 and you can drive the reaction by removing the CO2.
DeleteUnless Ca(OH)2 and H2CO3/HCO3- dissolved in water are involved, I doubt many chemists would call this an acid-base reaction. I'd call the reaction of HO- with CO2 a nucleophilic attack by hydroxide on the electrophilic carbonyl groups of CO2.
A lime kiln is obviously a complicated situation. Burning wood or coal produces both CO2 and H20 as byproducts in addition to the heat needed to drive the reaction.
Frank
Nick: Thanks for the post and references. I've wanted to learn something about this subject. As best I can tell, none of your basic chemistry determines what happens in the ocean. There should be simple equations calculating what the equilibrium pH should be with 300 ppm, 600 ppm, 1000 ppm or 180 ppm (LGM) of CO2 in the atmosphere, but those equations are missing. That's always suspicious. However, since much of the ocean is supersaturated with CaCO3, the principles of equilibrium chemistry are not necessarily relevant. What bothers me is that all of these organisms using calcium carbonate evolved hundreds of millions of years ago when atmospheric CO2 levels were much higher than today. If ocean acidification is really dangerous, how did these organisms come to exist? Interestingly, the pH inside cells and in the blood is 7.4, which might represent the pH of the water where life evolved.
ReplyDeleteHere are some basics that might help.
pH is -log10[H+] or pH is the additive inverse of the log base10 of the hydrogen ion concentration. Your discussion of Lewis acids is irrelevant to pH. The term acidity when it refers to pH (as it usually does in aqueous solutions). If you put a Lewis acid in water, it can result in the release of H+. For example, tri-coordinate boron species are Lewis acids:
B(OH)3 + H2O ==> B(OH)4- + H+
pKa is - log10(Ka)
If one takes the log10 of both sides of the equation defining Ka, [H][A]/[HA] = Ka, one get the following very useful relationship explaining the phenomena of buffering:
pKa = pH - log10([A]/[HA] and pH = pKa - log10([HA]/[A]
At pH 8.13 (near that of the ocean), the ratio of HCO3- to CO3-- is 10:1.
When equal amounts of HA and its conjugate base A are present, the pH is equal to the pKa. If one adds acid until the ratio is 10/1 (40% of [HA]+[A]), the pH is one unit less than the pKa. If one adds a little more acid (9% of [HA]+[A]) the ratio will be 10/1 and the pH will be two units less than the pKa. 0.9% more acid reduces the pH one more unit. The opposite is true for adding bases. A concentrated solution of a weak acid (or base) moderates changes in pH when the pH of the solution is near the pKa (or pKb) because then it takes a large amount of acid or base to change the log10([HA]/[A]. When the pH far from the pKa, a small amount of acid or base can change the pH several units. During the titration of bases, the pH of the solution often changes several pH units as one drop of strong acid is added converting the last molecules of A to HA.
Frank
Frank,
Delete"There should be simple equations calculating what the equilibrium pH should be with 300 ppm,"
Well, there's a plot, the last. It shows how everything varies with log([CO2]). The light blue line is pH.
Your buffer relations are the log of what I wrote in the section headed "Buffers". Yes, I probably should have written them again for the "pH Equilibrium relations" section. They are the basis for the Bjerrum plot (first one).
BTW, I see that the blogspot editor mangled by equilibrium signs - hope they are clearer now.
Nick,
ReplyDeleteI am not sure if I do understand your thoughts about the role of protons and CO2 correctly .
You write:
" But the H+ is created by the first reaction and destroyed by the (back) second reaction"
and:
"I'm saying that in seawater, the aprotic Lewis acid CO2 dissolves CaCO3. Protons are involved as intermediates"
Do you mean that the main driver for dissolution of CaCO3 is CO2, and that protons act as catalysts?
So, when I put solid CaCO3 in a properly buffered solution of pH 8.0 and then raise pCO2 to e.g. 600 ppm. Do you expect that more CaCO3 will dissolve (pH kept constant)?
I'm saying that H+ is not an independent part of the equilibrium chain. It's likle the various intermediates you get in chemical reactions - present in small amounts, and used as fast as it is created.
ReplyDelete"So, when I put solid CaCO3 in a properly buffered solution of pH 8.0 and then raise pCO2 to e.g. 600 ppm. Do you expect that more CaCO3 will dissolve (pH kept constant)?"
I'm saying you can't do that. [H+] and [CO2] are linked - approximately proportional - see the last 3 figs. That's true with bicarb buffering, but would be true of any effective buffer to pH 8. Any acid stronger than the buffer acid will have it's concentration controlled - not only [H+].
In fact, if you've been trying to get pCO2 up to 600 ppm in a solution pH 8 by adding CO2, you will have created a lot of bicarb and there will be a bicarb buffer in operation. And yes, more CaCO3 will have dissolved.
"I'm saying you can't do that. [H+] and [CO2] are linked".
ReplyDeleteWell thats why using a buffer. At 600 ppm atmospheric CO2, the dissolved CO2 concentrations will be less than 1 mM, bicarbonate less than 10 mM. This can be easily buffered by e.g. a 200 mM Tris buffer, pH 8.0.
But leaving technical problems aside, as a thought experiment to see if I understood you correctly:
Increasing pCO2 at constant pH, will that increase the dissolution of CaCO3?
Buffers don't hold anything constant. They stabilize. In a Tris solution in contact with CaCO3, you already have CO3-- in accordance with the solubility product, and HCO3- in equilibrium with that (at ph *) and even some CO2 (or H2CO3). If you add CO2, the CO2 will react with the Tris base, producing bicarb, and it will shift the buffer (Tris and HCO3-) equilibrium slightly. [H+] and [CO2} will increase in nearly the same proportion. As here, {CO3--] will drop in the same proportion without CaCO3, but will be replenished by dissolving CaCO3 if present.
ReplyDelete"Buffers don't hold anything constant, they stabilize"
ReplyDeleteHuh??? Well at least within measurable amounts it will keep the pH constant, that's what they are used for all over the world.
Still you didn't answer my question: if I could manage to keep the pH constant (in a pH-stat this is possible), and the [CO2] is increased, will more CaCO3 dissolve?
Anon,
DeleteI'll say it again - buffers don't hold anything constant. You can see this in my first plot - the Bjerrum plot. Say the green curve - that's the CO3--/HCO3- buffer. The slope isn't vertical. If you change anything, you change the pH. It buffers because you have to add a lot of reagent to get a modest change in pH.
You can read it off in the last plot - the blue line -pH varies with log(pCO2). The only way you can add CO2 and hold pH constant is to add a corresponding base as well. But then you might as well add the neutralised mix.
So your question has an impossible premise. You can't add CO2 and hold pH constant. You'll get a small drop and dissolve some CaCO3.
You can do the arithmetic without Tris from Fig 2 - the anlarged Bjerrum plot. Add CO2 - TA doesn't change but DIC increases. Work out the new RTA (from % change in DIC). Find the new y-location. That tells you the new pH. Tris only adds a minor complication. Alternatively you can read everything off the fourth plot.
The Bjerrum plot shows the ratios of the different carbonate species as function of pH. That is not relevant for the discussion about buffering.
ReplyDeleteWrt your statement " buffers don't hold anything constant", a calculation of the change in pH when a strong acid is added to a buffersystem
Buffer:
200 mM of the weak acid HA, pKa=5
200 mM of its conjugate base, the sodium salt NaA.
Equilibrium:
(i) HA <-> H+ + A- (pKa = 5.0; weak acid, only partly dissociated)
(ii) NaA --> Na+ + A- (sodium salt, completely dissociated)
NaA is completely dissociated --> [A-] = 200 mM.
The presence of [A-] will push the equilibrium of (i) further to the left hand side--> [HA] = 200 mM
Substituting the values for [HA],[A-]and pKa in the Henderson-Hasselbalch equation (pH = pKa - log HA/A-) yields the initial pH:
pH= pKa - log1 = 5.0
Effect of adding 1 mM of the strong acid HCl on the pH.
HCl--> H+ + Cl- --> 1 mM H+ + 1 mM A- --> 1 mM HA.
1 mM HA formed --> new concentration of HA = 201 mM,
1 mm A- consumed --> new concentration of A- = 199 mM.
pH=pKa - log 201/199 = 5 - 0.004 = 4,996.
A shift of 0.004 is not measurable (NB: 600 ppm atmospheric CO2 introduces less than 0.1 mM CO2). This change is sufficient small to separate the effect of H+ from that of CO2 on the CaCO3 solubility.
Anon,
DeleteLet's continue the calc. Say HA has pKa 8 - your calc is basically the same. But instead of HCl, we add HB, with pKa 5, with the aim of getting [HB] up to 0.001 M. That's like what you're asking for pCO2. Notation - I'll call pHB = -log([HB]) etc.
Then pA+pH=pHA+8. Initially pA=pB=-log(.2)=0.7
pB+pH=pHB+5
Add y=001mM HB, and let x=[HB] after reaction.
Then [B]=y-x
pH=5-log(x/(y-x))
Now we know that pH is still close to 8, so
log(x/(y-x))~-3, or x~1E-6 with y=.001.
So virtually all the HB has reacted; approx
[HA]=.2+y, [A]=.2-y (just as if HB had been HCl)
Again, pH=8+log(.199/.201)=7.996
So a small shift in pH, but also in [HB]. They are linked. Approx
pH=8+log((.2-y)/(.2+y))=8-4.34*y=5-log(x/(y-x))
change in pH = log((.2-y)/(.2+y))= -4.34*y
and x=0.001*y
So adding HB gives you a small change in pH, but also a small change in [HB]. If you want to reach a prescribed level of [HB] (pCO2), you have to add a whole lot of HB, and that makes a significant change to pH. For example, to get to [HB]=.1mM after reaction, you have to add .1M HB and the pH drops by 0.434.
Add y=001mM HB
Deleteshould be
Add y=0.001 M HB
Nick,
DeleteCO2 behaves differently from an ordinary weak acid HB, since it is in equilibrium with CO2 in the gas phase (Henry's law: [CO2]=0.03pCO2.
The concentration of CO2 and henceforth of H2CO3 (H2O+CO2 <-> H2CO3, K= 1.7x10^-3)are fixed by the atmospheric pCO2. At ambient pressure, assuming pCO= 3.5x10^-4 atm:
-->[CO2]water = approx 1x10^-5 M,
-->[H2CO3]= approx 2x10^-8 M .
pH = pKa - log [H2CO3]/[HCO3-];
pH=8.0
pKa = approx 3.7 (dissociation equilibrium of H2CO3<-> H+ + HCO3-)
log[H2CO3/[HCO3-] = -4.3; [H2CO3]=10^-7.7
--> [HCO3-] = 10^-3.4 = approx 4x10^-4 M.
To generate 4x10^-4 M HCO3- , 4x10^-4 M H+ must have been absorbed by the buffer. As calculated in my previous post, introduction of 1 mM H+ had no measurable impact on the pH of a 200 mM Tris buffer.
Anon,
Delete"CO2 behaves differently from an ordinary weak acid HB"
It's not different behaviour of the acid, it's the way you've prescribed the change. With HB, I followed your prescription of a small quantity (1mM) of acid added. That is, actually adding 1 millimol to each litre. The added acid is buffered much as H+ is. The rise in [H+] and [HB] are both small.
But if you provide a large source of HB (or CO2), at fixed pCO2, then indeed it can rise to be in equilibrium. But the amount that crosses the boundary is large. You mentioned going to 600 ppmv CO2, which raises [CO2] to 1 mM. But that doesn't men you've added 1 mM CO2. You had to add a whole lot more than that. And you will get a much larger drop in pH.
To put it another way, seawater is mainly a HCO3-/CO3-- buffer. In this context, CO2 is a strong acid (as it is relative to Tris). It is buffered in much the same way as H+. If you add enough CO2 to force a doubling of equilibrium pCO2, then it will be enough to also force a doubling of [H+]. That's not a small change.
Anon,
DeleteJust going through your calc, you get down to here:
"[HCO3-] = 10^-3.4 = approx 4x10^-4 M. "
As you say, you could get to that situation if you raised pCO2 to that level from zero, and some base absorbed the protons. But that isn't the situation. [HCO3-] in seawater is about 2 orders of magnitude higher. It's about 100x[CO2]. That's the equilibrium requirement. You're able to get pH 8 with pCO2=3,5E-4 atm by starving the solution of HCO3- to allow the equilibrium. But in seawater that isn't possible.
Nick: Figure 7 in Zeebe is created from a model of how the ocean will respond to CO2 WITH TIME. The simple principles of chemical equilibrium mentioned in your post don't vary with time. The long periods of time have nothing to do with how long it takes to reach chemical equilibrium, those periods are required for subduction and volcanic emission of CO2, the MOC, and are highly speculative.
ReplyDeleteThe ocean is supersaturated with CaCO3, which is slowly precipitating almost everywhere (including coral and other living things). To an unknown extent, this precipitating CaCO3 should be available to buffer changes in acidity. The pH of pure water in equilibrium with atmospheric CO2 is around 5. Now add an excess of powdered CaCO3. What will the new pH be at equilibrium? Then double atmospheric CO2 and calculate what happens. I'm confused as to why these discussions cover much of the basics, but not simple relevant calculations like this.
If you find them. please post.
Thanks for your post and reply, Frank
Frank,
DeleteYou can work it out thus:
With known [Ca++], from the solubility product you can work out [CO3--]
Then [H+]=K2*[HCO3-]/[CO3--]; K2=10^-9.13
and [H+]=K1*[CO2]/[HCO3-]; K1=10^-5.94
Eliminate [HCO3-]
[H+]^2=K1*K2#[CO2]/[CO3--]=K1*K2*[Ca++][CO2]/Ks
where Ks is the solubility product
2*pH = 9.13+5.94+log(Ks)-log[Ca++] -log[CO2]
I notice that my last equation there is just log mass action for anon's:
DeleteCO2 + H2O + Ca++ <-> CaCO3 + 2H+
So it was useful :)
Nick: As I recall, the usual procedure is to write out four equations to solve for the four unknowns: H+, HCO3-, CO3--, Ca++. You seem to be one equation short. Sometimes these equations are conservation equations, like: 2[Ca++] = [HCO3-] + 2{CO3--]. (Charge balance after starting with uncharged CO2 and CaCO3.) One can solve for each of these three terms in terms of K1, K2, Ks, and [CO2]. ASSUMING I didn't screw up the algebra, I get a fourth degree equation relating [H+] and [CO2]:
DeleteKs*[H+]^4 = (1/2)*K1^2*K2*[CO2]^2*[H+] + K1^2*K2^2*[CO2]^2
A quick glance at the your graph of ion composition vs pH says that at pH 8, [HCO3-] >> [CO3--]. Under these condition, the last term (for [CO3--]) can be omitted:
Ks*[H+]^3 = (1/2)*K1^2*K2*[CO2]^2
pH will then vary with 2/3 of the log of the change in [CO2]. In other words, each doubling of CO2 will cause an 0.2 drop in pH units.
For pH's where {CO3--] is the dominant inorganic carbon species, {H+] will vary with the square root of CO2 and a doubling of CO2 will cause a drop of 0.15 pH units.
So the change in pH per doubling or halving is 0.15-0.20 pH units, and much closer to 0.20 at current ocean pH and during future acidification from burning fossil fuels.
Your equation is correct for a situation where one assumes that [C++] is independent of [CO2]. This might apply in the ocean, which is supersaturated with CO2. The equilibrium fall in pH for doubling CO2 at constant [Ca++] would be 0.15 pH units. So 0.15-20 pH units per doubling is still right.
Ocean acidification doesn't need to be under equilibrium control. The supersaturation of CaCO3 proves that equilibrium hasn't been reached. So why discuss simple chemical equilibria in a review article when those principles don't apply? This appears to be another attempt to make complicated phenomena into "settled science".
It would be nice to check some of this work, but we need to know the units for [CO2]. I think the usual practice is to enter the concentration of gases in these equilibria equations in units of atmospheres, but I can't be sure what practice has been followed in your K1. The equilibrium constant formally has units associated with it, but these are often skipped. For [H][A]/[HA] = K, K usually has units of molarity (M). If HA is a gas, the units for K might be atmospheres, unless we know the molarity of the gas dissolved at equilibrium under a particular partial pressure of the gas.
Anon,
DeleteI think there are only three equilibrium equations (K1, K2, Ks), and these are the only ones that give absolute equations for concentrations. Your charge equation should be:
2Δ[Ca++] +Δ[H+] = Δ[HCO3-] + 2Δ[CO3--]
and it's true for changes, but in absolute terms you have to include [Na+] etc.
There are 7 species in the equations:
CO2 HCO3- CO3-- H2O H+ Ca++ CaCO3
and so it is possible to have 4 independent conservation equations. C, Ca, H and charge are one set. But because we don't want to deal with the activity of CaCO3 or H2O, these have to be eliminated, leaving two invariants:
DIC - [Ca++] and
TA - 2*{Ca++]
where again DIC = ]CO2] + [HCO3-] + [CO3--]
and TA = Total Alkalinity = [HCO3-] + 2*[CO3--] - [H+]
The addition of [Ca++] is needed to ensure that the solution is invariant to CaCO3 precipitation.
That's 5 equations in 5 unknowns, which is sufficient to determine a trajectory when CO2 is added.
Complete set of reactions
ReplyDelete(1) [CO2(dissolved)] = 0.03xpCO2 (pCO2 in units of atmosphere)
(2) H2O + CO2(dissolved) --> H2CO3; Kw = 1.7×10-3
(3) H2CO3 <--> H+ + HCO3– ; K= 2.5×10−4
(4) HCO3– <--> H+ + CO32- ; K= 5.6×10−11
(5) H2O <--> H+ + OH-; K=10-14
(6) CaCO3 <--> Ca2+ + CO32–; ; Ks = 9×10−9
(7) Electroneutrality condition: 2[Ca2+] + [H+] = [HCO3-] + 2[CO3--] + [OH]-
At ambient air pCO2 = 0.040 atm (approx).
(1) -->[CO2dissolved] = 1.4x10^-5 M (fixed)
(2) --> [H2CO3] = 2.4x10-8 M (fixed)
Anon,
DeleteThanks for those numbers. They don't quite agree with Zeebe, but I'll use them. I'll explain my earlier statement - you can't increase pCO2 and hold pH constant.
Notation - I'll write a vector p() of concentrations in pH style: -log([]). They'll be listed in the order you can determine them with your equations:
H2CO3, H+, HCO3-, CO3--, OH-, Na+.
I'm using Na instead of Ca to avoid worrying about precipitation. Just buffers.
Start with just water and pCO2=0.04. A rather acid solution. We need to add base (NaOH)to get pH to 8.2.
Then all the concentrations can be worked out successively with mass action, from your eqs (3-5) except for Na+, which comes from charge balance(7):
[Na+] + [H+] = [HCO3-] + 2[CO3--] + [OH]-
The answer is
p=(7.62, 8.20, 3.02, 5.07, 5.80, 3.01)
Note that HCO3- and Na+ are dominant.
Now suppose we increase pCO2 by 10% and hold pH=8.2. log10(1.1)=0.0414.
Then p=(7.58, 8.20, 2.98, 5.03, 5.80, 2.97)
Note that last figure - [Na+] has gone up. But no Na was added. That means charge balance failed.
A better estimate is that [HCO3-] remains unchanged, since it is approx [Na+]. From your 1, that means [H+] and [H2CO3] change in proportion. Redo the calc with pH=8.2-0.0414:
p=(7.58, 8.16, 3.02, 5.12, 5.84, 3.01)
Yes, now p(Na) is unchanged. We have charge balance. And [H+] is up by 10%, or pH down by .04.
Nick,
DeleteYour calc applies on the situation in seawater, without an external buffer. My claim is that in the presence of an external buffer (e.g. 200 mM Tris, pH=8.0)CO2 can be varied while keeping pH constant. In this setting the claim in your original post, (i.e. CO2 directly drives CaCO3 into solution, the role of H+ is overemphasised) can be tested. You maintain that this is not possible ("buffers don't hold anything constant"), oke fine. We can go on endlessly exchanging paper-chemical arguments, but that will not settle the issue, I'm afraid. The experiment will decide: I'll prepare a Tris buffer (pH = 8.0) and expose it to a 5% CO2 atmosphere for a day or so and measure its pH afterwards. (I'll have to use a pCO2 of 5%, because the experiment is done in a cell culture incubator. When I lower the pCO2 down to 0.0004 atm, my PhD students will kill me).
Anon,
DeleteThat's great - I'll look forward to hearing. My current rather rough prediction (ignoring CO3--) for 200 mM Tris at pH=pKa 8, 0.05 atm CO2 is pH=7.8.
Anon,
DeleteOn working on a more general algorithm, I think I made a mistake in that early estimate, and that the equilibrium after exposure to 5% by vol CO2 should be pH 7.48.
Then [HCO3-]=0.052 M, [Tris_acid]=0.154 M, [Tris_base]= 0.046 M, [CO3--]=0.0011 M , with fixed [CO2]=0.0015 M. I'm assuming pKa=8 for Tris, 5.94/9.13 for CO2/HCO3-/CO3-- (Zeebe).
I'll have to postpone the experiment. The incubator broke down over the weekend. :-(
DeleteSorry to hear that. Good luck with fixing it.
DeleteNick and Anon: I agree that the charge conservation equation should be as shown below. Thanks for the correction.
ReplyDelete2*[Ca++] + [H+] = 2*[CO3--] + [HCO3-] + [OH-]
The problem I originally intended to solve asked what pH an aqueous solution with excess solid calcium calcium would have in equilibrium with an "infinitely large" atmosphere with differing amounts of CO2. This is the kind of question that could also be answered with an experiment. The large excess of CO2 allows us to treat [CO2] as a constant (a situation which may not apply to the ocean). The activity of solid CaCO3 and H2O are both one by convention, so we now have five equations and the five unknowns in the above conservation of charge equation. We can solve for each term in the conservation of charge eqn in terms of K1, K2, Kw, Ks, [H+] and [CO2] and obtain a relationship between [CO2] and [H+]. Getting rid of all the fractions afford five terms with units of M^6, including [H+]^4 and [CO2]^2, which is unlikely to have an analytical solution. As above, we can hypothesize that some terms will be negligible at some pH's, eliminate those terms and see if the solution is compatible with the hypothesis.
So let's assume that the pH will end up where [HCO3-] >> [CO2] and [CO3--] and also assume that [Ca++] >> [H+]. This affords:
2*[Ca++] ~= [HCO3-]
2*Ks*[H+]^2/K1*K2*[CO2] ~= K1[CO2]/[H+]
[H+]^3 ~= {K1^2*K2/2*Ks}*[CO2]^2
As described above, under these conditions, doubling CO2 will reduce pH by 0.2 units. Using pCO2 = 0.0004 atm (not 0.04 atm above) and Henry's constant for CO2 dissolving in water 29.41 atm/M, gives [CO2] = 1.32E-5 M (same as Anon). The apparent ionization constant for CO2 (the product of the real ionization constant and Keq for hydration) is 4.16E-7. This affords a pH of 8.36 (consistent with the hypothesis that bicarbonate is the dominant anion, 1.29E-3 M) and [Ca++] = 6.47E-4 M (confirming that it is the dominant cation).
The charge balances within 3%, so this is a reasonable approximation.
Frank (who forgot his name at least once)
Thanks, Frank,
DeleteMy new project is to try to make a graphic calculator, so you can slide the CO2 button up and down, say, and see everything else change. If I can get it going I'll post a draft version.
You may want to include a number of caveats. The calculation we did assumed that the atmosphere has an infinite supply of CO2 that will maintain a constant pCO2 (say as CaCO3 is added) or total CO2 was added to both the atmosphere and the solution (as CO2, HCO3- and CO3--) to produce a given pCO2. We also assumed that there was an infinite supply of solid CaCO3 available to replenish CO3--. This may not be as unreasonable as it sounds, but some of this excess is CaCO3 in coral reefs and other organisms. The high ionic strength in the ocean requires equilibrium constants appropriate for this situation. The worst problem is how to deal with the supersaturation (usually called omega) with respect to calcium carbonate. I suspect you may want to allow omega as an input to be multiplied by the equilibrium constant for dissolution of CaCO3).
ReplyDeleteIt suddenly dawns on me that I'd like to know both the decrease in pH and the increase in soluble Ca++ as pCO2 increases. "Ocean acidification" sounds bad, but "calcium carbonate dissolution" may be the real issue. However, there is no excuse for calcium carbonate to dissolve where omega is above one.
If you limit yourself to the assumption that [Ca++] ~= 2*[HCO3-], I'd want to calculate the concentration of the other cations and anions to prove that the error in this assumption still produces a solution with roughly equal amounts of cations and anions. If you reduce pCO2 enough, [CO3--] will become significant and if you increase it enough (Venus?), the assumption that Ca++ is the dominant cation could breakdown. (It's hard to imagine having excess CaCO3 in acidic solutions where their is little CO3--.) If you want to avoid such limitations, the full equation to be solved (by repeated approximation?) I got was:
2*[Ca++] + [H+] = [HCO3-] + 2*[CO3--] + [OH-]
2*Ks*[H+]^3/K1*K2*[CO2] + [H+] =
K1*[CO2]/[H+] + 2*K1*K2*[CO2]/[H+]^2 + Kw/[H+]
Frank
Frank,
DeleteI think the calculator should not do CaCO3 precipitation. As you say, supersaturation is very hard, and also just the heterogeneous distribution of CaCO3 in the ocean..
It may also not be a real issue. It seems to me that the key requirement for Ca skeletons is that they are never exposed to dissolving conditions, which probably requires a reserve of supersaturation.
I doubt if Ca exchange with living organisms is on a large enough scale to greatly affect open ocean chemistry. There is the other aspect of replenishment of Ca++ from inorganic CaCO3.
Nick: It is your calculator, so do what you want. As best I can tell, the default omega should be 1, but it can't really be wrong to allow the user to change it. I certainly don't understand the implications and misunderstanding that might develop from allowing users to change this parameters. Perhaps these will be clarified by comments from users.
ReplyDeleteAs best I can tell, using omega = 1 simulates the situation in the most sensitive regions of the planet where increasing pCO2 will reduce [CO2--] and potentially liberate more Ca++. Thus my interest in the amount of Ca++ liberated rather than acidification itself.
The lifetime of many organisms that use calcium carbonate is very short, so they may be an important source of CaCO3. Other forms of calcium carbonate like coral may dissolve very slowly. And we shouldn't forget that may organisms - people included - actively transport Ca++ to the locations where they want CaCO3 to precipitate (as bones and teeth).
Frank
Frank,
ReplyDeleteThe mineral phase of bone and teeth (enamel) is calciumhydroxyapatite, Ca10(PO4)6(OH)2, not CaCO3. Bone is a living tissue, which is continuously in turn-over, whereas tooth enamel is acellular (> 95% mineral) and cannot be repaired by the body when damaged. Spontaneous dissolution of enamel is prevented by saliva, which is oversaturated wrt calciumhydroxyapatite. When pH drops below approx 5.0, tooth enamel starts to dissolve.
Anonymous: Thanks for correcting my mistakes. Do you happen to know how we get hydroxyapatite to precipitate where we want it to? 1) Active transport of Ca++ or phosphate to increase the local concentration. 2) Active transport of hydrogen ions to increase pH and the ratio of tribasic phosphate to other phosphate species.
ReplyDeleteFrank
Frank,
ReplyDeleteBone formation is a multifactorial complex process, and there is debate about the nitty gritty of the mechanism. There is, however, agreement on the general principles. This is based on a large number of experimental data.
First should be noted that mammalian tissue fluids are supersaturated in calcium and phosphate ions, so the challenge for the body is to prevent precipitation of calciumphosphate salts rather than to enhance it. Uncontrolled precipitation of calciumphosphate salts throughout the body is prevented by a number of inhibitors which complex with calcium ions, lowering its free concentration. Inhibitors can be inorganic ions (e.g pyrophosphate), organic ions (e.g. citrate) and proteins (e.g. alfa fetuin).
Below I give a VERY simplified description of the processes involved.
The following conditions must be fulfilled for mineralization to occur:
(i) presence of a suitable extracellular matrix.
(ii) low concentrations of mineralization inhibitors.
(iii high local concentrations of free calcium and phosphate ions.
(i) Osteogenic cells synthesise an extracellular matrix consisting of collagen fibers. This matrix function as a lattice in which calciumphosphate salts are deposited. (Btw the coral skeleton is also composed of a mineralized extracellular matrix).
(ii) Osteogenic cells pinch of vesicles (sac-like structures) which diffuse into the collagen matrix. Anchored to the outside of the vesicles is alkaline phosphatase. This enzyme hydrolyses pyrophosphate to phosphate:
--> [pyrophosphate] will decrease --> [free Ca++] will increase; [phosphate] will increase.
(iii) The vesicle membrane contains also protein-pores which selectively let through calcium- and phosphate ions. Other ions and proteins cannot enter the inside of the vesicle. Phosphate and calcium ions diffuse into the vesicle and precipitate, forming nanocrystals of calcium phosphate.
The concentrations of free calcium and phosphate ions inside the vesicle are lower than outside the vesicle, so diffusion and precipitation will continue until the vesicle burst. CaP nanocrystals are released inside the collagen matrix, forming nucleation cores for further mineralization.
In an alternative mechanism is proposed that deposition of calcium phosphate occurs directly in the matrix, but the trigger is essentially the same: removal/degradation of inhibitors.
There seems to be quite an explosion of "ocean chemistry denialism" in recent weeks, starting at WUWT and propagating elsewhere. I noticed it from a thread at Richard Telford's blog (link). Some of his commentators are working hard to muddy the waters. Anyway, there seems to be a fairly sudden increase in the volume of misinformation being written about ocean acidification.
ReplyDelete