There has been another round of the bizarre theories of Pat Frank, saying that he has found huge uncertainties in GCM outputs that no-one else can see. His paper has found a publisher - WUWT article here. It is a pinned article; they think it is a big deal.
The paper is in Frontiers or Earth Science. This is an open publishing system, with (mostly) named reviewers and editors. The supportive editor was Jing-Jia Luo, who has been at BoM but is now at Nanjing. The named reviewers are Carl Wunsch and Davide Zanchettin.
I wrote a Moyhu article on this nearly two years ago, and commented extensively on WUWT threads, eg here. My objections still apply. The paper is nuts. Pat Frank is one of the hardy band at WUWT who insist that taking a means of observations cannot improve the original measurement uncertainty. But he takes it further, as seen in the neighborhood of his Eq 2. He has a cloud cover error estimated annually over 20 years. He takes the average, which you might think was just a average of error. But no, he insists that if you average annual data, then the result is not in units of that data, but in units/year. There is a wacky WUWT to-and-fro on that beginning here. A referee had objected to changing the units of annual time series averaged data by inserting the /year. The referee probably thought he was just pointing out an error that would be promptly corrected. But no, he coped a tirade about his ignorance. And it's true that it is not a typo, but essential to the arithmetic. Having given it units/year, that makes it a rate that he accumulates. I vainly pointed out that if he had gathered the data monthly instead of annually, the average would be assigned units/month, not /year, and then the calculated error bars would be sqrt(12) times as wide.
One thing that seems newish is the emphasis on emulation. This is also a WUWT strand of thinking. You can devise simple time models, perhaps based on forcings, which will give similar results to GCMs for one particular variable, global averaged surface temperature anomaly. So, the logic goes, that must be what GCM's are doing (never mind all the other variables they handle). And Pat Frank's article has much of this. From the abstract: "An extensive series of demonstrations show that GCM air temperature projections are just linear extrapolations of fractional greenhouse gas (GHG) forcing." The conclusion starts: "This analysis has shown that the air temperature projections of advanced climate models are just linear extrapolations of fractional GHG forcing." Just totally untrue, of course, as anyone who actually understands GCMs would know.
One funny thing - I pointed out here that PF's arithmetic would give a ±9°C error range in Hansen's prediction over 30 years. Now I argue that Hansen's prediction was good; some object that it was out by a small fraction of a degree. It would be an odd view that he was extraordinarily lucky to get such a good prediction with those uncertainties. But what do I see? This is now given, not as a reduction ad absurdum, but with a straight face as Fig 8:
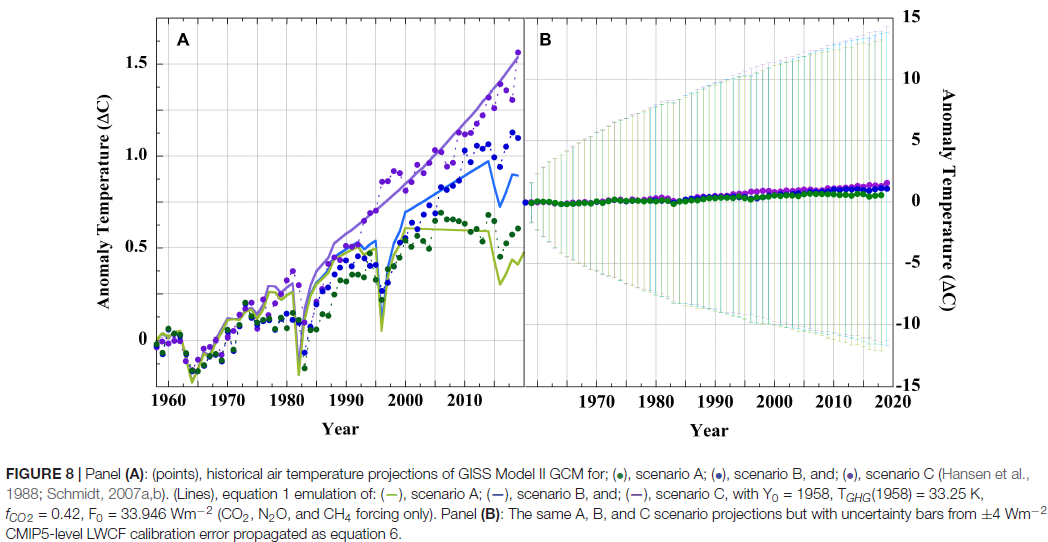
To give a specific example of this nutty arithmetic, the paper deals with cloud cover uncertainty thus:
"On conversion of the above CMIP cloud RMS error (RMSE) as ±(cloud-cover unit) year-1 model-1 into a longwave cloud-forcing uncertainty statistic, the global LWCF calibration RMSE becomes ±Wm-2 year-1 model-1. Lauer and Hamilton reported the CMIP5 models to produce an annual average LWCF root-mean-squared error (RMSE) = ±4 Wm-2 year-1 model-1, relative to the observational cloud standard (81). This calibration error represents the average annual uncertainty within the simulated tropospheric thermal energy flux and is generally representative of CMIP5 models."
There is more detailed discussion of this starting here. In fact, Lauer and Hamilton said, correctly, that the RMSE was 4 Wm-2. The year-1 model-1 is nonsense added by PF, but it has an important effect. The year-1 translates directly into the amount of error claimed. If it had been month-1, the claim would have been sqrt(12) higher. So why choose year? PF's only answer - because L&H chose to bin their data annually. That determines GCM uncertainty!
Actually, the ±4 is another issue, explored here. Who writes an RMS as ±4? It's positive. But again it isn't just a typo. An editor in his correspondence, James Annan wrote it as 4, and was blasted as an ignorant sod for omitting the ±. I pointed out that no-one, nor L&H in his reference, used a ± for RMS. It just isn't the meaning of the term. I challenged him to find that usage anywhere, with no result. Unlike the nutty units, I think this one doesn't affect the arithmetic. It's just an indication of being in a different world.
One final thing I should mention is the misunderstanding of climate models contained in the preamble. For example "Scientific models are held to the standard of mortal tests and successful predictions outside any calibration bound. The represented systems so derived and tested must evolve congruently with the real-world system if successful predictions are to be achieved."
But GCMs are models of the earth. They aim to have the same physical properties but are not expected to evolve congruently, just as they don't evolve congruently with each other. This was set out in the often misquoted IPCC statement
"In climate research and modelling, we should recognise that we are dealing with a coupled non-linear chaotic system, and therefore that the long-term prediction of future climate states is not possible. The most we can expect to achieve is the prediction of the probability distribution of the system’s future possible states by the generation of ensembles of model solutions. This reduces climate change to the discernment of significant differences in the statistics of such ensembles. "
Update - I thought I might just highlight this clear error resulting from the nuttiness of the /year attached to averaging. It's from p 12 of the paper:

Firstly, of course, they are not the dimensions (Wm-2) given by the source, Lauer and Hamilton. But the dimensions don't work anyway. The sum of squares gives a year-2 dimension component. Then just taking the sqrt brings that back to year-1. But that is for the uncertainty of the whole period, so that can't be right. I assume Pat Frank puts his logic backward, saying that adding over 20 years multiplies the dimensions by year. But that still leaves the dimension (Wm-2)2 year-1, and on taking sqrt, the unit is (Wm-2)year-1/2. Still makes no sense; the error for a fixed 20 year period should be Wm-2.












Thank you for your input to wuwt. But please do not give up on them. They are pushing this document like no other and the likes of trump will believe. Perhaps quotes of your debunk would be better - is a whattie likely to follow a link - I think not!!
ReplyDeleteWell then you'd be wrong thefordprefect. I like Nick and his contributions are always welcome at WUWT. Many at WUWT like Nick.
ReplyDeleteFrom
Global Climate Models and Their Limitations
http://solberg.snr.missouri.edu/gcc/_09-09-13_%20Chapter%201%20Models.pdf
We see that the models are indeed constrained to give a sensible result.
"Observational error refers to the fact that instrumentation cannot measure the state of the atmosphere with infinite precision; it is important both for establishing the initial conditions and validation. Numerical error covers many shortcomings including “aliasing,” the tendency to misrepresent the sub-grid scale processes as largerscale features. In the downscaling approach, presumably errors in the large scale boundary conditions also will propagate into the nested grid. Also, the numerical methods themselves are only approximations to the solution of the mathematical equations, and this results in truncation error. Physical errors are manifest in parameterizations, which may be approximations, simplifications, or educated guesses about how real processes work. An example of this type of error would be the representation of cloud formation and dissipation in a model, which is generally a crude approximation.
Each of these error sources generates and propagates errors in model simulations. Without some “interference” from model designers, model solutions accumulate energy at the smallest scales of resolution or blow up rapidly due to computational error."
It is odd that they name reviewers without letting us see their reviews (that I can find)... e.g., we have no idea whether Carl Wunsch said "this paper isn't worthy to be my dog's breakfast!" (which I hope he did), or, "my god, I had no idea all the climate modeling I've done is so worthless - thank you for enlightening me, great sir!" (which I highly doubt).
ReplyDelete-MMM
According to a comment at WUWT, Pat has seen the rewiews, so unless they are subject to some kind of NDA, he could quote them (or paraphrase) online if he so chose....
DeleteThe reviews are linked in the WUWT article.
DeleteWell I haven't followed every link, but I can only see a file of reviews of previous papers. I would be particularly interested in seeing what Carl Wunsch wrote, where can I find that pls?
Delete- According to wiki:
ReplyDelete"In October 2015, Frontiers was added to Jeffrey Beall's list of "Potential, possible, or probable" predatory open-access publishers.[5][37][10] The inclusion was met with backlash amongst some researchers.[5] In July 2016 Beall recommended that academics not publish their work in Frontiers journals, stating "the fringe science published in Frontiers journals stigmatizes the honest research submitted and published there",[38] and in October of that year Beall reported that reviewers have called the review process "merely for show"
And, writing about a chemtrails conspiracy article published in a Frontiers journal, Beall wrote: "The publication of this article is further evidence that Frontiers is little more than a vanity press. The fringe science published in Frontiers journals stigmatizes the honest research submitted and published there.
I suspect that no honest publisher would have accepted this article. That’s why conspiracy theorists such as Herndon go to MDPI and Frontiers when they want to publish something — the acceptance and publication are all but guaranteed, as long as the author fee is paid.
Frontiers’ peer review process is flawed. It is stacked in favor of accepting as many papers as possible in order to generate more revenue for the company. Frontiers is included on my list, and I recommend against publishing in its journals, which are rather expensive to publish in anyway."
https://web.archive.org/web/20160809165213/https://scholarlyoa.com/2016/07/14/more-fringe-science-from-borderline-publisher-frontiers/
https://en.wikipedia.org/wiki/Frontiers_Media#cite_note-38
Publishing fees seem to be the thick end of 2K USD, hope you got your money's worth, Pat!
Oh, boo hoo. Typical paid opinion by Phil Clarke Then there's Fordie whining over the participation of Wunsch, while simultaneously trying to claim the journal is no good. Do you really think he's allow his name to go on as a reviewer if the paper was "nutty" as Stokes claims?
ReplyDeleteClarke argues that it's pay for play and therefore the publisher can't be trusted. Go look at fees for Nature and many others that offer open access.
But every one of you lamers was TOTALLY OK with Lewandowsky publishing his unethical psychoanalysis paper there, which was later retracted because people like me spoke up about it and the abhorrent practices he used. None of you did, not one. You were totally OK with the "science" in Frontiers then.
"I suspect that no honest publisher would have accepted this article. That’s why conspiracy theorists such as Herndon go to MDPI and Frontiers when they want to publish something — the acceptance and publication are all but guaranteed, as long as the author fee is paid." Well golly, that's just what happened to Lewandowsky with his conspiracy theory paper.
In April 2013, Frontiers in Psychology retracted a controversial article linking climate change denialism and "conspiracist ideation"; the retraction was itself also controversial and led to the resignations of at least three editors. (Boo hoo, they defended bad science that nobody else would publish.)
It's all about hate and tribalism with you folks. There's no honesty about science with any of you, especially the ones hiding behind fake names.
Feel free to be as upset as you wish.
Oh dear.
DeleteIf anybody cares, I use my real name and (of course) never been paid to post.
PS Say hi to Smokey for me, I kinda miss the old hypocrite :-)
DeleteSounds a little tu quoque-ish to me.
DeleteTo quoque - if I ever feel the need of an alias, I'll use that.
DeleteIt would be very poetic - Et tu, Quoque?
DeleteExcellent critique of the paper, btw.
Take it to PubPeer where the flaws in the paper will live on in infamy:
ReplyDeletehttps://pubpeer.com/publications/391B1C150212A84C6051D7A2A7F119
WUWT is mostly nonsense; it basically is to climate science, what a flat-Earther blog is to Earth science. It's not a place to go to learn about science, with comments from Nick Stokes', Steve Mosher's, etc. being the exceptions.
ReplyDeleteAnyway, I think it would be worthwhile to mention some previous rebuttals to Frank's dubious claims, in case people wanted to learn more. Patrick Brown has a good discussion below:
https://youtu.be/rmTuPumcYkI
https://andthentheresphysics.wordpress.com/2017/10/23/watt-about-breaking-the-pal-review-glass-ceiling/
And for those who want to read up on some of the published evidence on model skill in representing cloud responses, lest Frank mislead them on that as well:
"Evidence for climate change in the satellite cloud record"
"Cloud feedback mechanisms and their representation in global climate models"
"Observational evidence against strongly stabilizing tropical cloud feedbacks"
"A net decrease in the Earth’s cloud, aerosol, and surface 340 nm reflectivity during the past 33 yr (1979–2011)"
"On the response of MODIS cloud coverage to global mean surface air temperature: Ts-mediated cloud response by MODIS"
Frank's piece is so bad it shouldn't have even have been published in a peer-reviewed science journal, and I wouldn't mind it being retracted. That's not unjustified censorship, since peer-reviewed science journals are not meant to be a place where any random nonsense is published.
And I forgot to mention Frank's false forecast of a continuing pause in global warming. Funny that he messed up on that, since he's now falsely claiming that GCM are largely useless for forecasts, even though they forecasted a continuing warming trend that he failed to:
Deletehttps://tamino.wordpress.com/2011/06/02/frankly-not/
https://web.archive.org/web/20180104193244/https://wattsupwiththat.com/2011/06/02/earth-itself-is-telling-us-there%E2%80%99s-nothing-to-worry-about-in-doubled-or-even-quadrupled-atmospheric-co2/
Franks is out to lunch I suspect. However, the truth of the matter is not very comforting either.
ReplyDelete1. Weather models use various spectral approximations followed by "filtering" out of undesirable "wiggles." This process is always subject to instability if the filtering is not strong enough in some situation. Modern upwind methods are preferable in that they have proofs of stability at least for simple hyperbolic systems. However, they are not perfect either.
2. There is little theoretical reason to suspect that numerical errors will remain small over time. It's all case dependent and dependent on the Lyopanov constants for that case.
3. In any case classical methods of numerical error control fail in any chaotic time accurate simulation. Thus there is essentially no knowledge about the role of numerical errors vs. subgrid models of turbulence and convection, etc. vs. real bifurcations and saddle points.
This matters less in weather simulations but in climate simulations where you do millions of time steps, it might matter a lot. No one knows though.
David Young can't seem to reconcile the fact that large scale fluid dynamics (i.e. low wavenumber with respect to earth's circumference) can be analytically solved and matched to observations, with his own inability to solve turbulence models that occur on the trailing edge of an airplane wing. Too bad, we don't care.
DeleteWell Paul, I've been over this with you in great detail at Science of Doom recently. I'll just say that you are sadly uninformed about fluid dynamics and the large effect of turbulence.
DeleteIf you are talking about Rossby waves, they are indeed much easier than many other flows. However, many other very important aspects of the climate system are indeed very difficult or indeed ill-posed. Convection and clouds are two examples.
David Young, A blog comment section is not considered "great detail". You are no Terry Tao.
DeleteWouldn't the propagation of errors over millions of time steps result in chaotic end results fairly regularly? Perhaps the fact that GCM runs remain generally stable speaks against this concern.
DeleteWell barry the results are chaotic. The climate patterns are all over the place as Science of Doom's latest post demonstrates. The global average temperature anomaly is fairly consistent because of conservation of energy and tuning of top of atmosphere flux. Ocean heat uptake is usually roughly right too. But energy balance methods also get these things right. Everything else we really care about is all over the place.
DeleteThe results are not chaotic, contrary to what this unpublished dude is saying. The variability in the climate signal is predominately due to ENSO and the other oceanic dipoles. These are equally as stable as the tides but only slightly more difficult to predict based on the tidal equations.
DeleteFrom Slingo and Palmer:
Delete"Figure 12 shows 2000 years of El Nino behaviour simulated by a state-of-the-art climate model forced with present day solar irradiance and greenhouse gas concentrations. The richness of the El Nino behaviour, decade by decade and century by century, testifies to the fundamentally chaotic nature of the system that we are attempting to predict. It challenges the way in which we evaluate models and emphasizes the importance of continuing to focus on observing and understanding processes and phenomena in the climate system. It is also a classic demonstration of the need for ensemble prediction systems on all time scales in order to sample the range of possible outcomes that even the real world could produce. Nothing is certain."
This reflects what experts in fluid dynamics (in virtually all fields of application) say.
Slingo and Palmer are LOL hysterical. Reading that quote, it's clear that they're only saying their simulation is chaotic. This is the mistake you geniuses always make. A Lyapunov exponent can only be estimated for a mathematical formulation, but never on actual data. This means that it's very difficult to distinguish chaos from a complex yet non-chaotic waveform.
DeleteTo paraphrase Jesse Ventura, chaos is a crutch for the weak-minded
PP, You are of course denying the basic facts of fluid dynamics here. All high Reynolds number flows are chaotic because of turbulence. There are also usually larger structures like vortex sheets/cores as well or convective shear chaotic shear layers. Slingo and Palmer are on very very solid scientific ground here.
DeleteYour discovery of LaPlace's tidal equation is a nothing burger. Simple models sometimes work for chaotic systems provided they include key nonlinear elements. That's a head fake for the naive like yourself because these models only work in their calibrated regimes and sometimes not even there.
You would learn more if you dropped the denial, the dissembling and the shameless self-promotion. If what you say is true, you could produce an ENSO forecest. You have never done so. Thus your assertions are just posturing so far as I can tell.
David Young, Hold my beer while I go look it up in my "LaPlace" transform tables, LOL
Deletebarry said: "Wouldn't the propagation of errors over millions of time steps result in chaotic end results fairly regularly? Perhaps the fact that GCM runs remain generally stable speaks against this concern.
ReplyDeleteYes. You can watch this for some insight. The talk is about using 16-bit resolution to solve the equations. This means the epsilon resolution is not critical
https://youtu.be/wp7AYMWlPLw
Watch the last few minutes to see the questions and comments from the audience.
"Things tend to look more chaotic than they actually are"
IEHO a major impediment to rational discussion is the elevatin of a single parameter, global temperature anomaly, which although informative, only captures a small part of what we measure and know.
ReplyDeleteRe: Annual means (+/- 4 W/sqm)
ReplyDeleteI see that on page 3833, Section 3, Lauer starts to talk about the annual means. He says:
“Just as for CA, the performance in reproducing the
observed multiyear **annual** mean LWP did not improve
considerably in CMIP5 compared with CMIP3.”
He then talks a bit more about LWP, then starts specifying the means for LWP and other means, but appears to drop the formalism of stating “annual” means.
For instance, immediately following the first quote he says,
“The rmse ranges between 20 and 129 g m^-2 in CMIP3
(multimodel mean = 22 g m^-2) and between 23 and
95 g m^-2 in CMIP5 (multimodel mean = 24 g m^-2).
For SCF and LCF, the spread among the models is much
smaller compared with CA and LWP. The agreement of
modeled SCF and LCF with observations is also better
than that of CA and LWP. The linear correlations for
SCF range between 0.83 and 0.94 (multimodel mean =
0.95) in CMIP3 and between 0.80 and 0.94 (multimodel
mean = 0.95) in CMIP5. The rmse of the multimodel
mean for SCF is 8 W m^-2 in both CMIP3 and CMIP5.”
A bit further down he gets to LCF (the uncertainty Frank employed,
“For CMIP5, the correlation of the multimodel mean LCF is
0.93 (rmse = 4 W m^-2) and ranges between 0.70 and
0.92 (rmse = 4–11 W m^-2) for the individual models.”
I interpret this as just dropping the formality of stating “annually” for each statistic because he stated it up front in the first quote.
He's probably binning annually. That just means you collect annual subsets as your way of estimating something ongoing. It doesn't change the thing you are estimating, and it certainly doesn't change the units.
DeleteSuppose you want to know how well your wind turbine is doing. So you calculate average output over week. 150 kW. Not 150 kW/week. Maybe try for a month. 120kW. Not 120 kW/month. Maybe put together 12 monthly averages. That's 130kW. Not 130 kW/month, because you binned in months. Nor 130 kW/year. That average is 130 kW/
Sounds ok for that example. But power output is not an uncertainty. This is the main weak point in his analysis (which I still believe is correct). I think he could use 4 w/sqm monthly also, for 100 years divide by sqrt(1200) instead of sqrt of (100). The average uncertainty at any given time over all the model runs is 4 W/sqm. That is not much relative to solar irradiance (say 1360 W/sqm). You would want to use a reasonable timeframe, and 1 year is reasonable for 100 years of prediction. Since we want to propagate the uncertainty, we have to include the effect of i-1 in i.
ReplyDelete"I think he could use 4 w/sqm monthly also, for 100 years divide by sqrt(1200) instead of sqrt of (100)."
DeleteWell, he could but he'd get a different answer. What is the use of an analysis that gives a different answer with whatever time period you choose, and your choice is arbitrary?
Of course, the real answer is that he shouldn't be accumulating at all. There is no basis for doing so, and he doesn't give one. I'm just pointing out the contradictions in the approach, which are an adequate proof that you can't do it that way.
The question is more about propagation of the uncertainty, for which you need to know the "shape" of the uncertainty. If the 4 W/m2 raises the temp by 0.1 oC per year, and it stays at 4 W/m2 every year, so, the question is, can it stay at the max or min for an extended period, or is it truly random - or random over time.
DeleteIf there are natural cycles driving the uncertainty that the model or mean input aren't accounting for, you would have to characterize all that to know. From a purely theoretical "all possible worlds" scenario, the uncertainty should propagate to the output over time at the max width, but that scenario is probably very low probability. It should be a 'probability gradient' rather than just a cone, if you will.
I try to transform the concept of error propagation into the real climate system. So the development of cloud cover percentage would behave like a particle's dislocation due to brownian motion. Is that realistic? Of course not! Cloud cover is part of the global water cycle that takes about a week. When a cloud has rained out at a specific location, the "next" condensation process is not (or maybe only weakly) correlated to the state before. Also the aerosols have been washed out. There is no longtime mechanism of cloud cover accumulation. And the proposed idea of error propagation even allows negative cloud cover - that's totally unphysical. Cloud cover on a longer timescale is related to balance and not to random shifts.
ReplyDeleteIf you're trying to measure something that's in W/m^2, and your uncertainty is in W/m^2/year, that means your measurements are getting worse each year.
ReplyDeleteI.e., you say a forcing is 20 W/m^2, +/- 4. Your measurement is 95% likely within 16-24 W/m^2.
If you add "/year", then that means next year, your estimate of forcing will be 20W/m^2 +/- ~7. And the year after that, 20, +-10, roughly. And so on.
Does the uncertainty in the measurements grow each year? No, it definitely does not. The units here are incorrect.
Wow, lots of ad homineming here. This site should be renamed "trashtalkers.com"
ReplyDeleteSee, I'd fit right in, but I gotta go now.
In case anyone is interested, I've been discussing this with Pat Frank over at PubPeer.
ReplyDelete**********************
Me:
**********************
Let's say that I measured the temperature outside my house over the course of a year and the annual average was 10 C. According to you, that is actually 10 C/year.
Now let's do a simple unit conversion. 10 C/year x 10 year/decade = 100 C/decade. According to you, the decadal average temperature outside my house is 100 C.
That would be nuts.
In the real world, averaging doesn't introduce any new units. You sum the measured quantities (preserving their units) and divide by the (unitless) number of measurements. Units remain unchanged.
**********************
Pat's reply evades the "unit conversion" point I was making; instead, he turns to use of an (inappropriate) analogy:
**********************
Pat Frank:
**********************
In your example, your 10 C/year would merely imply that the next year average may be near 10 C as well.
After 100 years, one could calculate a 1-year average from 100 years of data and see how closely your first year average came to the estimate from a larger data base.
Let me make it easy for you with a more homely example. You own an apple orchard. After harvest, you have 100 baskets of apples. You count the apples and discover that the average is 100 apples per basket. Per basket, Piper. Averages make no sense without that 'per.'
If we take your approach, we'd decide that after 100 years of harvests, every basket would include 100x100 = 10,000 applies. That's your logic. It produces utter nonsense.
**********************
It seems to me that he really does not understand what he's saying. In Pat's example, if there is an average of 100 apples in one basket, then there would be an average of 1000 apples in 10 baskets. But that doesn't work with the temperature case -- if the temperature averages 10 C in one year, it does NOT average 100 C in 10 years.
Thus my reply:
**********************
Me:
**********************
OK, let's apply the unit-conversion test to your apples example.
You have measured an average of 100 apples in each basket. If we define a "decabasket" as 10 baskets, then the following can be used to extrapolate our estimate of the number of apples per basket:
100 apples/basket x 10 baskets/decabasket = 1000 apples/decabasket
That looks good to me. But now try it with the temperature example, using your claim that my front yard's annual mean temperature of 10 C is actually 10 C/year:
10 C/year x 10 year/decade = 100 C/decade
10 C/year x 0.083 year/month = 0.83 C/month
So according to Pat Frank, the average temperature in my front yard is simultaneously 10 C ("per year") and 100 C ("per decade") and 0.83 C ("per month").
Weird, huh? The answer is quite simple. Pat's "apple" example really IS about rates: the "average" that is being estimated is the average rate of apples per basket. But the "temperature" example IS NOT about rates. Pat doesn't understand this and so he turns it into a rate by appending a spurious "per year" unit to the quantity "10 C".
The unit-conversion test is a handy way of demonstrating the problem with Pat's work here. If your work falls apart when you try to apply simple unit conversions, it means you're doing it wrong.
**********************
Piper,
DeleteI have had similar discussions, eg here, where he said, yes, the annual average temperature at London would be properly given the units °C/year. Leter he tries to walk back.
There was an interesting addendum here where I noted that his units were actually quite inconsistent. Despite all the table thumping, he more frequently writes the relevant quantity as ±4 Wm⁻² than ±4 Wm⁻² year⁻¹, and lately the year⁻¹ has been fading rapidly. Importantly, when he actually uses it, in Eq 5.2, it is ±4 Wm⁻², and wouldn't make sense otherwise. His reply is a doozy.
With this stuff, you try to peel away one level of nuttiness, and there are whole new layers beneath.
Another part of the difference is that baskets and apples are discrete quantities. You can have 1 basket; you can't have really have 2.3 baskets or 3.14 baskets. But temperature and time are continuous quantities.
DeleteWhen you have an average over a discrete quantity (say, the average height of a group of people), it is implicitly about the unitted quantity. It is the height of a person.
When you have an average of temperature over days, weeks, months, you're measuring temperature at given points in time, interpolating between those, and your average is the integral of this temperature function, divided by the time. Same rough idea, but discrete vs continuous.
The same way that average height of a group of people has "of a person" as the implicit attached unit, an average temperature has "at a moment in time" as the implicit attached unit. Not over a month, or a year, but at an instant.
Discrete vs. continuous.
"has "of a person" as the implicit attached unit"
DeleteCareful, this is getting into Frank territory. And its not an SI unit.
I think the right way to think of an average Av(x) is to perform a linear operation A(x), then divide by A(1), so Av(1)=1. Generally A(x)=∫w x dx, say, so you divide by ∫w dx. The units are those of x, noting extra implied. The extra unit introduced by integration cancels out. It's the same with summation.
Hi,
ReplyDeleteThe economics blog, EconLog, posted Pat Frank's theories with approval. I and others tried to point out some of the flaws.
https://www.econlib.org/archives/2016/12/hooper_and_hend_2.html
https://www.econlib.org/archives/2017/04/henderson_and_h.html
One thing in particular that I pointed out was that satellite and balloon measurements also show warming. He was not persuaded (needless to say ;-)).