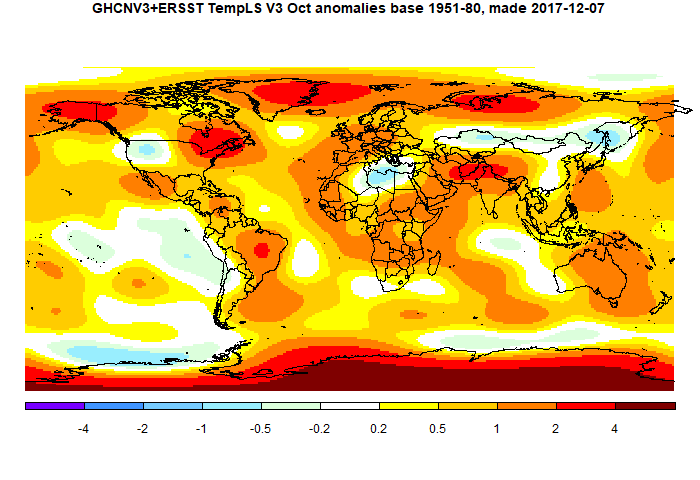
I dealt with a rather similar occurrence of this issue last year. There I showed an example where Melbourne daily maxima given to 1 decimal (dp) were averaged over a month, for several months, and then averaged again after rounding to nearest integer. As expected, the errors in averaging were much less than 1°C. The theoretical is the standard deviation of the unit uniform distribution (sqrt(1/12) approx 0.29, divided by the sqrt of the number in the average, and the results were close. This time I did a more elaborate averaging with a century of data for each month. As expected this reduced the error (discrepancy between the 1dp mean and the 0dp mean) by a factor of 10.
I also showed here that for the whole process of averaging over time and globally over space, adding white noise to all monthly averages of amplitude 1°C made almost no difference to the global anomaly time series.
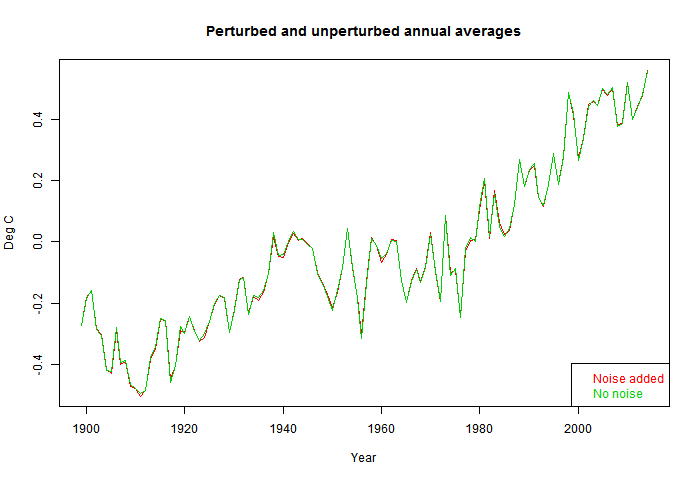
The general response that there is something special about the measurement errors which would make them behave differently to the rounding change. And there are usually arguments about whether the original data was really as accurate as claimed. But if one could somehow have perfect data, it would just be a set of rather similar numbers distributed over a similar range, and there is no reason to expect rounding to have a different effect. Nor is there any kind of variation that could be expected to have different effect to rounding, as long as there is no bias; that is, as long as the errors are equally likely to be up or down. If there is bias, then it will be propagated. That is why bias should be the focus.
Here is a table of contents for what is below the fold: