In April, there was a big story summarized by a headline in the Telegraph:
"Top Scientists Start To Examine Fiddled Global Warming Figures"
I wrote about it here. The GWPF announced an inquiry into global temperature adjustments. They had assembled a panel of apparently reasonably well qualified scientists. They promulgated terms of reference (which seemed to borrow heavily from the terminology of Paul Homewood). They put out a call for submissions, with a deadline of 30 June. They said
"After review by the panel, all submissions will be published and can be examined and commented upon by anyone who is interested."
and set up a page for this purpose here. All this promptly echoed, eg here and here.
I immediately thought about putting in a submission, and did in fact write one. I sent it to the prescribed email address on 2 June. No response. So I emailed again to ask if it had been received, on 14 June. Still nothing. So then I wrote to the GWPF general email, and got a prompt and courteous response from none other than Andrew Montford. He said he couldn't find my submission there, so I sent him a copy, which he received. Encouraging.
Still no response from the actual panel though. I kept an eye on the site, especially the submissions page. I thought they might say that they had received (with thanks) x submissions, or some such. But AFAICS, the site didn't change at all.
There was one link on the page that said "news", which was an obvious place to try, but it didn't seem to connect to anything. Three months later, still wondering, I got a helpful direct link from a correspondent, to this page. And there I find, dated July 22, this information:
"The team has decided that its principal output will be peer-reviewed papers rather than a report.
Further announcements will follow in due course."
So...no report! So what happens to the terms of reference? The submissions? How do they interact with "peer-reviewed papers"?
And of course one may ask who (if anyone) will ever write those papers? And about what?
I wonder what changed their minds?
BTW, here is a Wayback snapshot from June. I don't think anything has changed, except for the "news".
Friday, September 25, 2015
Tuesday, September 22, 2015
Better gridding for global temperature
Computing global temperature is an exercise in spatial integration with scattered data. I have written a lot about it previously, eg here or earlier here. A spatial integral is a weighted average, so it comes down to calculating the weights. With TempLS, I first used a grid method, as is traditional. Then, to overcome the problem of empty cells, I used an irregular triangular mesh, as in finite element integration. I have also developed, and will soon describe, a method using spherical harmonics. I think the later methods are better. But grids also have some advantages, and I have long wanted to get a rational infilling basis.
You might ask - why bother with different methods, rather than finding just one good one? The answer is with this idea of reaching an invariant zone. If we can find an integral estimate that agrees over several different methods, that will give the greatest confidence in the result.
I'll give details, with the infill process, and tests of the improvement of the results, using spherical harmonics, below the fold. And of course there will be the usual WebGL active picture. It will show the cube grid projected on the sphere, and infill for a typical month, with lines to show the infill dependency.
The cell area on the sphere, which is what is needed for area weighting, is simple. The area on the cube face cell centered at r is reduced by the cos of a view angle, which is 1/|r|, and by the inverse square of the projection, which is |r|^-2, being a total factor of |r|^-3. And all those face cells have equal area on the cube.
If I was actually doing the integration, I would then multiply those cell average values by the cell areas and add them up. That would end up being a weighted sum of the data. For TempLS, I just want those weights. That is just accountancy. Every time one of the original cell values is used in another cell, I increase its weight.
As a matter of practicality, I limit this, so cells are deemed to inherit values from the four closest actual readings. "Closest" is determined by the stage at which they were associated in the diffusion process. For the cells that were not reached until the third or later stages, there are some arbitrary cutoffs, but the cells chosen should still be close.
In the plot below, for the TempLS data (GHCN+ERSST) for April 2015, you see first the populated cells with a colored checkerboard, different colors for each cube face. Note how the cells do not differ hugely in size, but shrink near the 8 cube corners. Stations reporting in April are marked with black dots. Then the infilled cells are marked in drab colors - grey for the first level, then brown, bluish etc. I'm using here a 24x24 grid on each face. That is finer in parts than the usual 5° lat/lon grid, and since the SST is on a 4° lat/lon in TempLS, there are gaps in sea temp as well. I've used this finer mesh to show multiple layers in the diffusion.
In the unpop (drab) cells, you see little white lines from the centres. These show the connections to the actual pop cells from which they are averaged.
I tabulate the results below, as a sum of squares of differences between the matrix of results and the unit matrix. I have broken into columns according to the L value. The number there is actually an average for products in that section, so it is in fact a power spectrum (more on this in future posts). You can think of L as rising (spatial) frequency. In any case, the test of good integration is that the numbers should be small. I have left out L=0, because that is zero by normalization.
The all grid integration is accurate to six figures. That reflects that the mesh is fine enough (24x24) to resolve these functions well. For the rest, infilling makes a dramatic improvement, by nearly two orders of magnitude, though arguably the square root should be the criterion. Both deteriorate at higher frequency, infilling at a faster rate.
Numerical integrtaion
Integration is usually defined as a limiting process, whereby the region is subdivided into finer and finer regions, which can then each be evaluated with some local estimate of the integrand. There is theory about whether that converges. With a finite amount of numerical data, you can't go to a limit. But the same idea applies. You can subdivide until you get a result that seems to depend little on changing the subdivision. Sometimes that won't happen before you run out of data to meaningfully estimate the many subdivisions. That's one reason why temperature anomalies are important. With absolute temperature, you would have to divide very finely indeed to be independent of topographic variation, and there just aren't enpigh reading locations to do that. But anomalies take out a lot of that variation, making practical convergence possible.You might ask - why bother with different methods, rather than finding just one good one? The answer is with this idea of reaching an invariant zone. If we can find an integral estimate that agrees over several different methods, that will give the greatest confidence in the result.
Grid considerations
With gridding, you can choose a coarse grid so that every cell has data. But then the data may not be a good estimate of the whole grid area. You lose resolution. A finer grid will start to have cells with no data. Traditionally, these are just omitted, meaning in effect that they are assumed to have the global average value. This was improved by Cowtan and Way 2013, using kriging. I proposed a simpler approach using latitude band averaging, which gave some of the same benefit. In this post I'll look at upgrading the infill process, using numnerics similar to solving the diffusion equation. It tries to find a local average to use for each missing cell.Improving on lat/lon grids
To do this, I need a better grid system than lat/lon. That creates a big problem at the poles, where cells become very small and skewed. The essential requirement of a grid is that you can quickly allocate a set of scattered data to the right cells, and you know the area of the cells. There are many other ways of doing this. Lat/lon is based on gridding the sphere as if it were a flat surface, which it very much isn't. You can do much better using a somewhat similar 3D object. Regular platonic polyhedra are attractive, and an icosahedron would be best of these. But a cube is more familiar, and good enough. That is what I'll use here. The cube is gridded in the normal way, with a square grid on each face. The sphere surface is radially projected onto the cube.I'll give details, with the infill process, and tests of the improvement of the results, using spherical harmonics, below the fold. And of course there will be the usual WebGL active picture. It will show the cube grid projected on the sphere, and infill for a typical month, with lines to show the infill dependency.
Cubic grid
Think of a Rubik style cube, but with finer gridding. I number each face by rows, with the numbering accumulating from face to face. I use a unit sphere and unit cube (each edge from -1 to 1). So a point (x,y,z) on the sphere projects to (x,y,z)/Max(|x|,|y|,|z|) on the cube. And to map back to the sphere, just divide by the magnitude.The cell area on the sphere, which is what is needed for area weighting, is simple. The area on the cube face cell centered at r is reduced by the cos of a view angle, which is 1/|r|, and by the inverse square of the projection, which is |r|^-2, being a total factor of |r|^-3. And all those face cells have equal area on the cube.
Diffusion
After allocating the data points to the cells by projection, I then have populated and unpopulated cells. Populated I estimate by the simple average of data in the cell. Then I check all the unpopulated that are next to one or more pop. They get the average of the adjacent cell values (cells that share an edge), and are marked populated. Then I repeat, until all cells are "populated".If I was actually doing the integration, I would then multiply those cell average values by the cell areas and add them up. That would end up being a weighted sum of the data. For TempLS, I just want those weights. That is just accountancy. Every time one of the original cell values is used in another cell, I increase its weight.
As a matter of practicality, I limit this, so cells are deemed to inherit values from the four closest actual readings. "Closest" is determined by the stage at which they were associated in the diffusion process. For the cells that were not reached until the third or later stages, there are some arbitrary cutoffs, but the cells chosen should still be close.
In the plot below, for the TempLS data (GHCN+ERSST) for April 2015, you see first the populated cells with a colored checkerboard, different colors for each cube face. Note how the cells do not differ hugely in size, but shrink near the 8 cube corners. Stations reporting in April are marked with black dots. Then the infilled cells are marked in drab colors - grey for the first level, then brown, bluish etc. I'm using here a 24x24 grid on each face. That is finer in parts than the usual 5° lat/lon grid, and since the SST is on a 4° lat/lon in TempLS, there are gaps in sea temp as well. I've used this finer mesh to show multiple layers in the diffusion.
In the unpop (drab) cells, you see little white lines from the centres. These show the connections to the actual pop cells from which they are averaged.
Test of integration
I've tested using spherical harmonics of order up to L=5 (36 functions). Products of these should integrate to produce an identity matrix (orthonormal). So I integrate, first using the grid as if all were present. Then I integrate using only the "populated" cells for that month of April. Then I integrate a third time infilling for the unpopulated cells. For those integrations I use the weighted formulation.I tabulate the results below, as a sum of squares of differences between the matrix of results and the unit matrix. I have broken into columns according to the L value. The number there is actually an average for products in that section, so it is in fact a power spectrum (more on this in future posts). You can think of L as rising (spatial) frequency. In any case, the test of good integration is that the numbers should be small. I have left out L=0, because that is zero by normalization.
| 1 | 2 | 3 | 4 | 5 | |
| Full grid | 0 | 0 | 0 | 0 | 1e-06 |
| Infilled grid | 8.8e-05 | 0.00029 | 0.001045 | 0.002015 | 0.003635 |
| No infill | 0.007632 | 0.027335 | 0.049327 | 0.064493 | 0.075291 |
The all grid integration is accurate to six figures. That reflects that the mesh is fine enough (24x24) to resolve these functions well. For the rest, infilling makes a dramatic improvement, by nearly two orders of magnitude, though arguably the square root should be the criterion. Both deteriorate at higher frequency, infilling at a faster rate.
Conclusion
Grid integration with diffusion infilling looks good, and may be competitive with triangle mesh. If so, this is welcome, because it manages things like land/sea separation more easily. I'll post more soon on comparisons of use in TempLS.Thursday, September 17, 2015
Land Sea interface in global temperature averaging
Inhomogeneity is a problem when estimating an average. You have to sample carefully. In political polling, for example, men and women tend to think differently. So you need to get the proportions right in the sample (or re-weight).
In a global temperature average, a big inhomogeneity is the land/SST difference. For grid-based estimates, a land mask is often used. This tells how much of each cell is land and how much sea.
I haven't used a land mask with TempLS grid, because I think grid weighting has bigger problems. And with mesh weighting, there isn't any clear way to mask, especially as there is typically a new mesh for each monthly set of stations.
The mitigation is that there is a lot of cancelling effects. Some land areas may be in effect represented by sea, but also vice versa. Island temperatures tends to influence surrounding sea, but then again, they really should. If they were only representative of their own land area, it would generally not be worth including them.
I may still try to do something more elaborate. But in the meantime, I thought I would test what the current algorithm does, using what maths call a color function. This is 1 (red) for land stations, 0 (blue) for SST. I plot it as if it were temperature. I hope to see that land areas uniformly red, sea blue, and an in-between color tracking the shore. Insofar as it fails to track, I hope the failure is balanced, so that neither sea nor land is over represented on average. The result is an active WebGL plot below the fold.
This is the plot for the stations reporting in March 2015. I think it is quite good. There is some intrusion of sea effect where land is poorly covered, and there is the expected smudging of islands, but generally the demarcation follows the coastlines.
In a global temperature average, a big inhomogeneity is the land/SST difference. For grid-based estimates, a land mask is often used. This tells how much of each cell is land and how much sea.
I haven't used a land mask with TempLS grid, because I think grid weighting has bigger problems. And with mesh weighting, there isn't any clear way to mask, especially as there is typically a new mesh for each monthly set of stations.
The mitigation is that there is a lot of cancelling effects. Some land areas may be in effect represented by sea, but also vice versa. Island temperatures tends to influence surrounding sea, but then again, they really should. If they were only representative of their own land area, it would generally not be worth including them.
I may still try to do something more elaborate. But in the meantime, I thought I would test what the current algorithm does, using what maths call a color function. This is 1 (red) for land stations, 0 (blue) for SST. I plot it as if it were temperature. I hope to see that land areas uniformly red, sea blue, and an in-between color tracking the shore. Insofar as it fails to track, I hope the failure is balanced, so that neither sea nor land is over represented on average. The result is an active WebGL plot below the fold.
This is the plot for the stations reporting in March 2015. I think it is quite good. There is some intrusion of sea effect where land is poorly covered, and there is the expected smudging of islands, but generally the demarcation follows the coastlines.
New sea ice treatment in TempLS
TempLS is my global temperature anomaly calculator. It uses ERSST V4 for the sea surface component. ERSST unhelpfully records sea covered with ice as having the sea water freezing point of -1.8°C. Since this does not seem to be a good proxy for air temperature, I mark such points as missing data.
However, it seems -1.8 is not reliable - regions which are clearly frozen can report higher temperatures. Maybe there is an allowance for salinity variation. Anyway, to date I have been using ≤-1°C as the criterion for removal.
I now find that helps, but also doesn't work reliably. Even with the Arctic ice near peak, there seem to be a few deviant points reporting SST where there should be none. This creates a problem with my triangular mesh weighting in the Arctic. The idea is that land stations should be a better basis (than -1.8) for estimating nearby frozen seas. But these isolated spurious sea temperatures also become prominent in the mesh, and affect large areas, as if they were land.
So I am using a new criterion. For each SST location and month, I look at the record starting 1900, and count the occurrences of temperatures less than -1.5°C. If there are more than 10, I deem the location to be subject to intermittent freezing, and exclude it for that month throughout.
This will clearly exclude some valid data on the fringes of the ice. However, with some years frozen, others not, it is in any case hard to get an appropriate normal. In practice the decision about inclusion does not have dramatic effects for individual locations, since freezing leads to a zero anomaly. And because it is a lat/lon mesh, there is an artificially high node density anyway.
You may notice some small differences in the TempLS mesh results. The August average rose from 0.7°C to 0.703 °C.
However, it seems -1.8 is not reliable - regions which are clearly frozen can report higher temperatures. Maybe there is an allowance for salinity variation. Anyway, to date I have been using ≤-1°C as the criterion for removal.
I now find that helps, but also doesn't work reliably. Even with the Arctic ice near peak, there seem to be a few deviant points reporting SST where there should be none. This creates a problem with my triangular mesh weighting in the Arctic. The idea is that land stations should be a better basis (than -1.8) for estimating nearby frozen seas. But these isolated spurious sea temperatures also become prominent in the mesh, and affect large areas, as if they were land.
So I am using a new criterion. For each SST location and month, I look at the record starting 1900, and count the occurrences of temperatures less than -1.5°C. If there are more than 10, I deem the location to be subject to intermittent freezing, and exclude it for that month throughout.
This will clearly exclude some valid data on the fringes of the ice. However, with some years frozen, others not, it is in any case hard to get an appropriate normal. In practice the decision about inclusion does not have dramatic effects for individual locations, since freezing leads to a zero anomaly. And because it is a lat/lon mesh, there is an artificially high node density anyway.
You may notice some small differences in the TempLS mesh results. The August average rose from 0.7°C to 0.703 °C.
Tuesday, September 15, 2015
Temperature change July to August mapped in GISS and TempLS
I was curious about the relatively small rise in the GISS August global land/ocean anomaly, relative to July. So I drew maps comparing gridded GISS with TempLS mesh for those months. The maps are based on a spherical harmonics fit to both data sets, with L=10 (121 functions). This puts them on exactly the same basis.
I included TempLS with GHCN adjusted data as well. This gives the opportunity to also show the differences between adjusted and unadjusted, and to plot the actual differences.
Nothing looked unreasonable. The big Jul-Aug difference between GISS and TempLS was in the treatment of Arctic (especially) and Antarctic. There is actually very little effect of GHCN adjustment. The month-month changes are themselves quite interesting; the patterns are quite persistent.
The GISS data I used was the 1200 km interpolated, (download gistemp1200_ERSSTv4). The TempLS runs used ERSST4 and GHCN from here. I fitted each set with spherical harmonics up to L=10 (121 functions). This gave enough resolution to make the comparisons, without risking artefacts.
In this tableau, for each set the July 2015 result is on the left, and August on the right. All data uses base years 1951-80, with conversion numbers from here.
Giss shows the Arctic going from part-warm to moderate everywhere. TempLS, however, has the Arctic warm in each month. In both datasets, East Antarctica is cold in both months, but generally a larger area in August. TempLS shows greater cooling in the East US. Both show the August warmth in S Americe, which is in fact the most noticeable change over the month.
You see a slight variation in SST with adjustment, which may seem odd, as only land is adjusted. But the spherical harmonic approx is global, so the effects can spread. The difference is small.
The next plot shows the actual differences Aug-July.
This emphasises the polar changes in GISS, with much less Antarctic change in TempLS, and almost none in the Arctic. A diffreence is not surprising, as GISS uses extra data in the south, and their interpolation scheme in the Arctic is also different. The other main differenve is in the US, where TempLS emphasises both the Eastern cooling and Western warming.
The next tableau shows the datasets differences, just for August.
Very little effect of GHCN adjustment, except for some in Antarctic. This is expected, because present time is the reference point for adjustment. The differences will be due to changes in the offsets. Between GISS and TempLS, you see another view of the polar differences, and otherwise just odd patches, mostly over land.
I included TempLS with GHCN adjusted data as well. This gives the opportunity to also show the differences between adjusted and unadjusted, and to plot the actual differences.
Nothing looked unreasonable. The big Jul-Aug difference between GISS and TempLS was in the treatment of Arctic (especially) and Antarctic. There is actually very little effect of GHCN adjustment. The month-month changes are themselves quite interesting; the patterns are quite persistent.
The GISS data I used was the 1200 km interpolated, (download gistemp1200_ERSSTv4). The TempLS runs used ERSST4 and GHCN from here. I fitted each set with spherical harmonics up to L=10 (121 functions). This gave enough resolution to make the comparisons, without risking artefacts.
In this tableau, for each set the July 2015 result is on the left, and August on the right. All data uses base years 1951-80, with conversion numbers from here.
 |  |
 |  |
 |  |
Giss shows the Arctic going from part-warm to moderate everywhere. TempLS, however, has the Arctic warm in each month. In both datasets, East Antarctica is cold in both months, but generally a larger area in August. TempLS shows greater cooling in the East US. Both show the August warmth in S Americe, which is in fact the most noticeable change over the month.
You see a slight variation in SST with adjustment, which may seem odd, as only land is adjusted. But the spherical harmonic approx is global, so the effects can spread. The difference is small.
The next plot shows the actual differences Aug-July.
 |  |
 |
This emphasises the polar changes in GISS, with much less Antarctic change in TempLS, and almost none in the Arctic. A diffreence is not surprising, as GISS uses extra data in the south, and their interpolation scheme in the Arctic is also different. The other main differenve is in the US, where TempLS emphasises both the Eastern cooling and Western warming.
The next tableau shows the datasets differences, just for August.
 |  |
 |
Very little effect of GHCN adjustment, except for some in Antarctic. This is expected, because present time is the reference point for adjustment. The differences will be due to changes in the offsets. Between GISS and TempLS, you see another view of the polar differences, and otherwise just odd patches, mostly over land.
Monday, September 14, 2015
GISS up by 0.06°C in August
GISS is out, and the land/ocean anomaly has risen from 0.75°C in July to 0.81°C in August. This is a smaller rise than I expected. It is similar to the 0.07°C rise I posted for TempLS mesh, but that has since crept up to 0.09.
The result is surprising to me, because GISS Ts, the land stations version, posted a very large rise of 0.22°C. Yet the analysis I posted for TempLS showed most of the rise accounted for by SST, with mostly stable land data portion. HADSST3 also rose.
There were some other oddities. GISS is posting a little earlier than usual, but unusually on a US Sunday, or at least that is when my data monitor picked it up. Yet the file was dated Friday 11th, which would be very early indeed.
The pattern of heat/cold is similar to that I have posted for NCEP/NCAR. Warmth in Middle East/Africa, but GISS has it right through W Europe too. Warmth in S America, and of course El Nino. Coolish in Antarctica and Central Russia. Maps below the fold.
Update. Some have suggested the Arctic melt season has ended. But in the Jaxa SIE record, two recent days of melting has taken 2015 to below, not only current 2011, but the 2011 minimum. Unless data is revised, that probably puts 2015 third behind 2012 and 2007. I think passing 2007 is unlikely.
Here is GISS for August:

And here is TempLS mesh (spherical harmonics):

The result is surprising to me, because GISS Ts, the land stations version, posted a very large rise of 0.22°C. Yet the analysis I posted for TempLS showed most of the rise accounted for by SST, with mostly stable land data portion. HADSST3 also rose.
There were some other oddities. GISS is posting a little earlier than usual, but unusually on a US Sunday, or at least that is when my data monitor picked it up. Yet the file was dated Friday 11th, which would be very early indeed.
The pattern of heat/cold is similar to that I have posted for NCEP/NCAR. Warmth in Middle East/Africa, but GISS has it right through W Europe too. Warmth in S America, and of course El Nino. Coolish in Antarctica and Central Russia. Maps below the fold.
Update. Some have suggested the Arctic melt season has ended. But in the Jaxa SIE record, two recent days of melting has taken 2015 to below, not only current 2011, but the 2011 minimum. Unless data is revised, that probably puts 2015 third behind 2012 and 2007. I think passing 2007 is unlikely.
Here is GISS for August:

And here is TempLS mesh (spherical harmonics):

Thursday, September 10, 2015
Spherical harmonics displayed
A few days ago, I noted that the climate debate was getting a bit quiet, and while keeping up with data etc, I would try also to talk a bit more about math. And I said a bit about how to implement spherical harmonics (SH), which I use in graphics.
Well, today I'd like to add a bit of color. I showed a Wiki illustration of the spherical harmonics. I thought that I could enhance the idea with some WebGL, and show higher orders (with world map added). So that is done here. You can choose between the orbital shapes, which are actually a kind of 3D polar plot, and just a surface shaded plot. The shapes are good for seeing the symmetries, but I think the shade plots may in the end be more informative.
I'm going to follow up further with SH. I'm using it for spatial integration, and I want to explore what can be done with spatial spectra. I'll blog about these soon. But for the moment, below the fold is the active WebGL display.
This plot is another variant of the generic sphere WebGL. It has the usual trackball capability. The options are
The idea of showing the world map is that the spacing of the SH lobes gives an idea of the scale of temperature effects that can be resolves. This works better in the shaded surface version than the orbitals.
Well, today I'd like to add a bit of color. I showed a Wiki illustration of the spherical harmonics. I thought that I could enhance the idea with some WebGL, and show higher orders (with world map added). So that is done here. You can choose between the orbital shapes, which are actually a kind of 3D polar plot, and just a surface shaded plot. The shapes are good for seeing the symmetries, but I think the shade plots may in the end be more informative.
I'm going to follow up further with SH. I'm using it for spatial integration, and I want to explore what can be done with spatial spectra. I'll blog about these soon. But for the moment, below the fold is the active WebGL display.
This plot is another variant of the generic sphere WebGL. It has the usual trackball capability. The options are
- 3D button - toggles between the orbital shape and shaded surface view
- Color - if you find the rainbow colors hurt your eyes, you can cycle through gentler alternatives
- L,M - a text box where you can write in values. Remember, L is the latitude parameter, M longitude, and |M|≤L. You can enter values directly if you like, with L from 0 to 12. Out of range values will just make the box go red. But you may prefer to use the colorful squares top right. It's an integer array with L as x-variable, M as y. Just click, and the numbers will appear in the text box, and the corresponding shape will show.
- Orient just restores the globe so the center line is N-S. "Plot New" probably won't be needed, unless you write in the LM text box directly.
The idea of showing the world map is that the spacing of the SH lobes gives an idea of the scale of temperature effects that can be resolves. This works better in the shaded surface version than the orbitals.
TempLS up 0.07°C in August
GHCN was late this month. I think the US Labor day weekend may have been the cause. However, today a lot of new data appeared, and Canada seems to be the only major one now missing. The TempLS mesh anomaly goes from 0.607°C in July to 0.679°C in August. That is a smaller rise than NCEP/NCAR (0.14°C), and does not make August as warm as Feb/Mar of this year. But it is still warm. A 0.07 rise would bring GISS to 0.82°C. Still noting NCEP/NCAR, I think GISS may rise more, though.
The smoothed map plot is here:

Warm spots in MidEast/Sudan, Central Europe, S America, Mongolia. Cool in E US. The map does not show it well but Antarctica was cold (even more than usual). The contribution plot from the report is here:

Much as in July, with SST continuing to rise, and being the main influence. Antarctica has been cool for some months.
Update. A commenter asked, which other recent months have been a record. Here is a table of years in which each month had the max value. I have colored cells where that month is the most recent with data:
The rowss Jan-Apr are relatively colorless. I think the reason is that there records tend to be at the El Nino peak, which we haven't yet reached. Maybe next year.
The smoothed map plot is here:

Warm spots in MidEast/Sudan, Central Europe, S America, Mongolia. Cool in E US. The map does not show it well but Antarctica was cold (even more than usual). The contribution plot from the report is here:

Much as in July, with SST continuing to rise, and being the main influence. Antarctica has been cool for some months.
Update. A commenter asked, which other recent months have been a record. Here is a table of years in which each month had the max value. I have colored cells where that month is the most recent with data:
| HadCRUT | GISSlo | NOAAlo | TempLSgrid | TempLSmesh | |
| Jan | 2007 | 2007 | 2007 | 2007 | 2007 |
| Feb | 1998 | 1998 | 2015 | 1998 | 2015 |
| Mar | 2002 | 2010 | 2015 | 2015 | 2010 |
| Apr | 2010 | 2010 | 2010 | 2014 | 2010 |
| May | 2015 | 2014 | 2015 | 2015 | 2014 |
| Jun | 2015 | 2015 | 2015 | 2015 | 2015 |
| Jul | 2015 | 2015 | 2015 | 2015 | 2015 |
| Aug | 2014 | 2014 | 2014 | 2015 | 2015 |
| Sep | 2014 | 2014 | 2014 | 2014 | 2014 |
| Oct | 2014 | 2014 | 2014 | 2014 | 2014 |
| Nov | 2013 | 2013 | 2013 | 2013 | 2013 |
| Dec | 2006 | 2006 | 2014 | 2014 | 2014 |
The rowss Jan-Apr are relatively colorless. I think the reason is that there records tend to be at the El Nino peak, which we haven't yet reached. Maybe next year.
Sunday, September 6, 2015
Spherical Harmonics
The climate blogging scene seems to be running out of steam. WUWT is mainly the same old posters with the same stories. Climate Audit blogs about football aeration. Lucia blogs about just about anything. So it seems an alternate topic is needed. I'll keep blogging about climate science, of course, but also maybe a bit about maths. It won't be click bait, but I hope there will be things worth discussing.
The maths for today is at least something I've been using, and I'll post a file which may be useful. I'm talking about spherical harmonics. These are functions orthogonal on a sphere, which can be used in the same way as you might use Fourier series. I use them for smoothing, and I'll be using them in future for integration.
I'll talk a little bit about where they come from - you can skip if you like. Then I'll show a method I now use for calculating them, with an associated table of coefficients that you can download.
The reason I've been looking at the methods aspect is that I wanted to do a Javascript implementation, for interactive use. I have long had a R implementation, which I've used for TempLS output. I use recurrence relations, to be described. It's not particularly hard to program, but easy to make mistakes. So, as I often do nowadays, I thought to pack the logic into a table of numbers which could be used with a simple mechanical program in any platform. I'll link the table. In the section below, you can skip all the math, which is not compulsory, and go straight to usage.
∇2Ψ = λΨ for some λ, on the whole sphere (no boundaries).
The reason they are orthogonal is similar to the orthogonality of eigenvectors of symmetric matrices (the Laplacian is self-adjoint). If
∇2Ψ1 = λ1Ψ1 and ∇2Ψ2 = λ2Ψ2, then integrating over the sphere
λ1∫ Ψ1 Ψ2 = ∫ ∇2Ψ1 Ψ2
= -∫ ∇Ψ1 . ∇ Ψ2 integrating by parts
= ∫ Ψ1 ∇ 2Ψ2
= λ2∫ Ψ1 Ψ2
So if λ1 != λ2, then
∫ Ψ1 Ψ2 = 0
Ylm=N Plm(sin(θ)) exp(i m φ) for l=0,1,2..., m=-l,...l, N a normalizing factor
Wiki displays them thus (attribution)
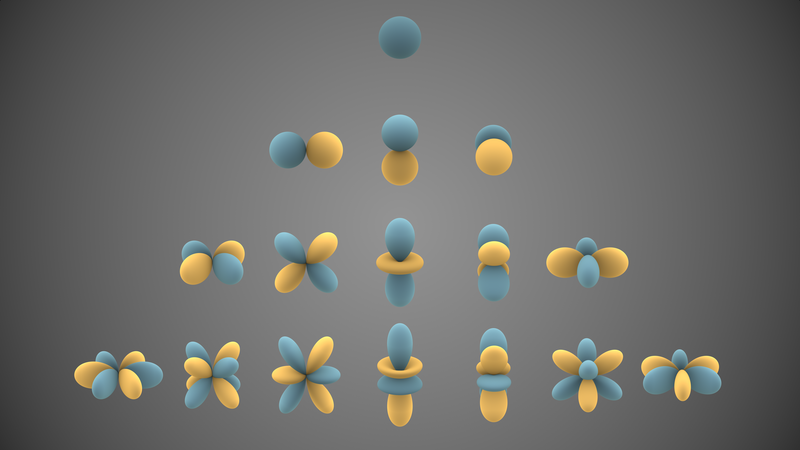
Visual representations of the first few real spherical harmonics. Blue portions represent regions where the function is positive, and yellow portions represent where it is negative. The distance of the surface from the origin indicates the value of in angular direction (Wiki)
You can think of it as a table, with Y00=1 at the top, m as the x variable and l as -y. This is the table that I compute.
A comment on the symmetries. As l increases, down the centre, each row brings an extra layer on the axis. As you go from that axis, you get one extra period around the equator, and one less along the axis. So the fourth row (l=3) end has three periods around the equator, and none along the polar axis. This increase of oscillations translates into ability to resolve variation. If you go to row 13, the period is about 30 degrees, so you can resolve variation on that scale.
For most, I use the relation connecting three consecutive l values (x=sin(θ)):

But this fails when m=l+1 - ie at end of rows. So then I use

relying on the last term being zero.
There are some variations. I don't use complex values, but rather the trig component cos(mφ) for m>0, and sin(mφ) for m<0. I calculate the trig formulae by summation, so that makes the edge formulae three-term again. And I modify the reduced relation to
Pm+1m+1 = -cos(θ) Pmm
absorbing the (2m+1) factor into the normalizer N.
So the implementation is just, successively, column i by column, H(1)=1,
c0 H(i)= s(j) c1 H(i1) + s(j+1) c2 H(i2)
s is an array consisting of (sin(θ), 1, cos(θ)cos(φ), cos(θ)sin(φ)), so j will be 1 or 3 (for row ends).
Here is a csv file of that table (transposed), with 441 columns, equivalent to 21 rows.
Here is an R usage:
You supply a set of lat/lon in degrees, and N+1 for number of rows, and you get an array H of orthonormal harmonics.
b = (HTH)-1(HTv)
for the coefficients, and then
V = H b
is the SH approximation. You can pick out terms or just display the smoothed approx. I am more enthusiastic now about using this for integration, when the coefficient b1 is the approximate integral (since H1 normalized is 1/4π and all other terms have zero integral. I think this method is almost as good as the mesh methods I use, and a lot faster (if stored weights are unavailable).
The maths for today is at least something I've been using, and I'll post a file which may be useful. I'm talking about spherical harmonics. These are functions orthogonal on a sphere, which can be used in the same way as you might use Fourier series. I use them for smoothing, and I'll be using them in future for integration.
I'll talk a little bit about where they come from - you can skip if you like. Then I'll show a method I now use for calculating them, with an associated table of coefficients that you can download.
The reason I've been looking at the methods aspect is that I wanted to do a Javascript implementation, for interactive use. I have long had a R implementation, which I've used for TempLS output. I use recurrence relations, to be described. It's not particularly hard to program, but easy to make mistakes. So, as I often do nowadays, I thought to pack the logic into a table of numbers which could be used with a simple mechanical program in any platform. I'll link the table. In the section below, you can skip all the math, which is not compulsory, and go straight to usage.
Origins
Spherical harmonics are eigenfunctions of the Laplacian on the sphere. That is, they are solutions of∇2Ψ = λΨ for some λ, on the whole sphere (no boundaries).
The reason they are orthogonal is similar to the orthogonality of eigenvectors of symmetric matrices (the Laplacian is self-adjoint). If
∇2Ψ1 = λ1Ψ1 and ∇2Ψ2 = λ2Ψ2, then integrating over the sphere
λ1∫ Ψ1 Ψ2 = ∫ ∇2Ψ1 Ψ2
= -∫ ∇Ψ1 . ∇ Ψ2 integrating by parts
= ∫ Ψ1 ∇ 2Ψ2
= λ2∫ Ψ1 Ψ2
So if λ1 != λ2, then
∫ Ψ1 Ψ2 = 0
Separation of variables
Using a coordinating system of the sphere consisting of latitude θ and longitude φ, we can use separation of variables to get two separate ordinary differential equations, for which θ and φ are eigenfunctions. The equation for φ is just the simple harmonic with trig function solutions. The equation for θ is a Legendre equation, for which the solutions are Associated Legendre polynomials Plm(sin(θ)). Together, the spherical harmonics areYlm=N Plm(sin(θ)) exp(i m φ) for l=0,1,2..., m=-l,...l, N a normalizing factor
Wiki displays them thus (attribution)
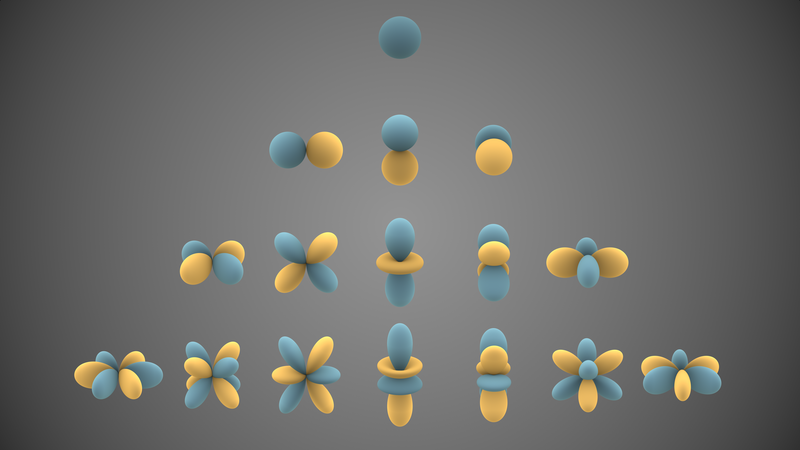
Visual representations of the first few real spherical harmonics. Blue portions represent regions where the function is positive, and yellow portions represent where it is negative. The distance of the surface from the origin indicates the value of in angular direction (Wiki)
You can think of it as a table, with Y00=1 at the top, m as the x variable and l as -y. This is the table that I compute.
A comment on the symmetries. As l increases, down the centre, each row brings an extra layer on the axis. As you go from that axis, you get one extra period around the equator, and one less along the axis. So the fourth row (l=3) end has three periods around the equator, and none along the polar axis. This increase of oscillations translates into ability to resolve variation. If you go to row 13, the period is about 30 degrees, so you can resolve variation on that scale.
Recurrence relations and array
Being essentially hypergeometric, there is a rich collection of three-term recurrence relations. I number the table by increasing m and then by L, ie by rows. I can compute any term provided I have a recurrence relation connecting it to two already known values. As an integer array, I can take any value out of the displayed cone (l≥0, |m|≤l) to be zero.For most, I use the relation connecting three consecutive l values (x=sin(θ)):

But this fails when m=l+1 - ie at end of rows. So then I use

relying on the last term being zero.
There are some variations. I don't use complex values, but rather the trig component cos(mφ) for m>0, and sin(mφ) for m<0. I calculate the trig formulae by summation, so that makes the edge formulae three-term again. And I modify the reduced relation to
Pm+1m+1 = -cos(θ) Pmm
absorbing the (2m+1) factor into the normalizer N.
Usage
So after all that, I assemble a table that I call hm, with 9 rows, and as many columns as harmonics required. If you include n rows from the table, there are n2 terms, and that number of columns required. The 9 rows are:- l
- m
- i2 pointer to recurrence location 3
- i1 loc 2
- j whether to use sin(θ) etc in recurrence
- c2 third coef in reccurence
- c1 second
- c0 first
- N normalizer.
So the implementation is just, successively, column i by column, H(1)=1,
c0 H(i)= s(j) c1 H(i1) + s(j+1) c2 H(i2)
s is an array consisting of (sin(θ), 1, cos(θ)cos(φ), cos(θ)sin(φ)), so j will be 1 or 3 (for row ends).
Here is a csv file of that table (transposed), with 441 columns, equivalent to 21 rows.
Here is an R usage:
hm=read.csv("https://s3-us-west-1.amazonaws.com/www.moyhu.org/blog/math/SHcoef.csv")
makeSH=function(la,lo,N){#Forms spherical harmonics YLM by implementing HM.
# la, lo are lat/lon in degrees
n2=(0:N+1)^2
N1=max(n2)
H=matrix(1,length(la),N1) # will be SH array
p2=pi/180
ss=cbind(sin(la*p2),1,cos(la*p2)*sin(lo*p2),cos(la*p2)*cos(lo*p2)); #
for(i in 2:N1){
m=hm[,i]; # hm is the table of coefs
H[,i]=(H[,m[4]]*m[7]*ss[,m[5]]+H[,m[3]]*m[6]*ss[,m[5]+1])/m[8]
}
for(i in 1:N1)H[,i]=H[,i]*hm[9,i]
H
}
You supply a set of lat/lon in degrees, and N+1 for number of rows, and you get an array H of orthonormal harmonics.
More usage
So what to do with it? Given any set of points (stations) on the sphere, and values v, you can project, regression wise:b = (HTH)-1(HTv)
for the coefficients, and then
V = H b
is the SH approximation. You can pick out terms or just display the smoothed approx. I am more enthusiastic now about using this for integration, when the coefficient b1 is the approximate integral (since H1 normalized is 1/4π and all other terms have zero integral. I think this method is almost as good as the mesh methods I use, and a lot faster (if stored weights are unavailable).
Thursday, September 3, 2015
Global surface August - NCEP/NCAR index up 0.14°C
Here are the results for the Moyhu NCEP/NCAR reanalysis index for August. It looked for a while to be a record breaking month, with steady warmth. But then there was a sudden late cool spell, apparently mostly Antarctica, and then an equally sudden recovery to warmth. The end result was 0.306°C, a big rise from July's 0.164. That is just slightly cooler (in this record) than May 2014 at 0.315°C. But it is the warmest for 2015 so far.
It makes a slight difference month-month what anomaly base period is used, and so the Moyhu table gives results also on the 1951-80 base (for GISS) and 1961-90 (NOAA Mlost). So the comparable GISS-base number would be 0.87°C. But as mentioned in earlier posts, the NCEP index, being air temperature, has been running rather cool relative to the land/ocean indices which using the warm current SST. So I would not be surprised if GISS were even higher - maybe even 0.9°C. The record GISS anomaly is Jan 2007 at 0.96°C.
ps This post is a little later than usual. The volatility meant that I wanted to go right to the end of month, and the last day of NCEP/NCAR was posted a little late at NOAA.
It makes a slight difference month-month what anomaly base period is used, and so the Moyhu table gives results also on the 1951-80 base (for GISS) and 1961-90 (NOAA Mlost). So the comparable GISS-base number would be 0.87°C. But as mentioned in earlier posts, the NCEP index, being air temperature, has been running rather cool relative to the land/ocean indices which using the warm current SST. So I would not be surprised if GISS were even higher - maybe even 0.9°C. The record GISS anomaly is Jan 2007 at 0.96°C.
ps This post is a little later than usual. The volatility meant that I wanted to go right to the end of month, and the last day of NCEP/NCAR was posted a little late at NOAA.
Wednesday, September 2, 2015
Sea ice melt
Neven has the full story, but the Arctic ice extent is still reducing; area not so much. The JAXA SIE has 2015 now below 2007, but still well above 2012. Whether it will finish below the 2007 minimum is unclear, since 2007 continued melting for a long time. But either second place or third looks likely.
In the same table, NSIDC has 2015 fourth, but just behind and likely to overtake 2011, which did not melt much in September.
In the Antarctic, NSIDC SIE had been briefly rising, but now some melt again. It's below all years since 2008.
In the same table, NSIDC has 2015 fourth, but just behind and likely to overtake 2011, which did not melt much in September.
In the Antarctic, NSIDC SIE had been briefly rising, but now some melt again. It's below all years since 2008.
Subscribe to:
Posts (Atom)











