TempLS correlation with other indices.

Since June 2011 I've been posting monthly TempLS global averages, before the other surface indices appear. The purpose of this haste is partly to see how well it performs in comparison, uninfluenced by "peeking". Here is a recent monthly comparison, with links to earlier months. I post the data here.

So it's now time for a review on how well TempLS tracks. Along the way, I found some interesting results on how the main indices track each other.

Data plot

The data sources are:
HADCrut 4
Gistemp Land/Ocean
NOAA Global Land Ocean
RSS MSU Lower Troposphere
UAH Lower Troposphere
and TempLS. The data is tabulated here

So here's a plot of the indices for those 17 months, set to a common anomaly base period of 1979-2000. Generally the surface-based (non-satellite) follow each other pretty closely:


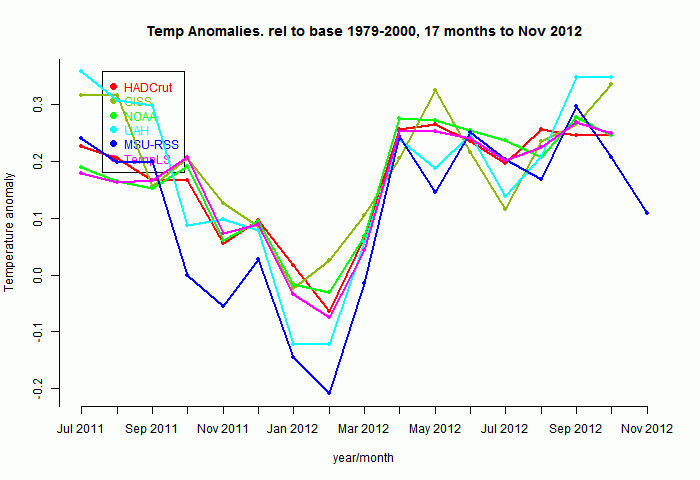
Now to show more detail of the differences, I'll plot the monthly differences between TempLS and the others. I'll arbitrarily zero the plots in a staggered way to make a point:



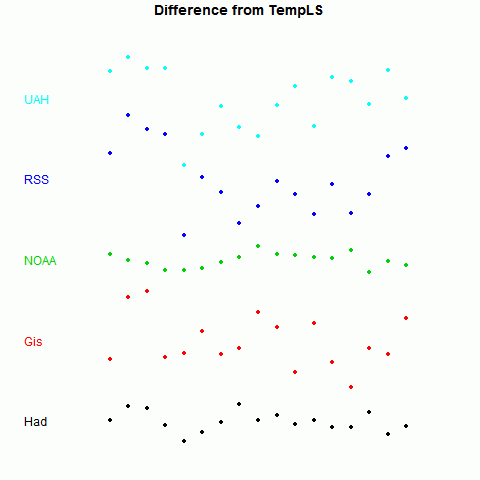
Now it becomes clearer. TempLS tracks NOAA very well, HADCrut 4 a little less, GISS less again, and the lower troposphere indices rather poorly.

There is, of course, a good reason for this. TempLS and NOAA use very similar datasets - GHCN land data, and ERSST. TempLS uses unadjusted GHCN, but there is very little adjustment in this time frame.

Quantification

I wanted to see also how the other indices track each other, and to give a statistically testable measure. An obvious one is just the standard deviation of the scatter seen in the figure above. Here is a table of that measure for each pairing:

Standard Deviations of differences (°C)

	Had	Gis	NOAA	RSS	UAH	TLS
Had	0	0.0579	0.0274	0.0836	0.0721	0.0248
Gis	0.0579	0	0.0692	0.0825	0.1017	0.0653
NOAA	0.0274	0.0692	0	0.0925	0.0756	0.0183
RSS	0.0836	0.0825	0.0925	0	0.0561	0.0867
UAH	0.0721	0.1017	0.0756	0.0561	0	0.0754
TLS	0.0248	0.0653	0.0183	0.0867	0.0754	0

The differences are marked - 0.0183°C for NOAA vs 0.0653°C for GISS, relative to TempLS.

Another measure is the correlation coefficient ρ for the monthly changes. This has the advantage that it can be easily tested for significance, with the formula for t-value:

t = ρsqrt((n-2)/(1-ρ*ρ))
where n is number of months. As usual, t is significantly above zero at 95% confidence if it exceeds 1.96. Actually, the significance is diminished by autocorrelation etc. Still, in cases of interest it clears that level by a wide margin.

Correlation coefficients of monthly changes   Had Gis NOAA RSS UAH TLS Had 0 0.594 0.845 0.601 0.678 0.923 Gis 0.594 0 0.423 0.404 0.148 0.505 NOAA 0.845 0.423 0 0.549 0.722 0.968 RSS 0.601 0.404 0.549 0 0.874 0.599 UAH 0.678 0.148 0.722 0.874 0 0.71 TLS 0.923 0.505 0.968 0.599 0.71 0

t-value of monthly changes Had Gis NOAA RSS UAH TLS Had 0 2.76 5.92 2.81 3.45 8.99 Gis 2.76 0 1.75 1.65 0.56 2.19 NOAA 5.92 1.75 0 2.46 3.9 14.43 RSS 2.81 1.65 2.46 0 6.74 2.8 UAH 3.45 0.56 3.9 6.74 0 3.77 TLS 8.99 2.19 14.43 2.8 3.77 0

The correlation of TempLS with all the indices is significantly positive, although with GISS barely so, over this period

Here's a graphical representation of the correlation. The circle areas are proportional to the t-value of the pairing. Big means close tracking. In fact, the area is proportional to ρ*sqrt(1/(1-ρ*ρ)); there's no difference for one plot, but it means that when I compare to different periods, the circles do not inflate with the longer period.
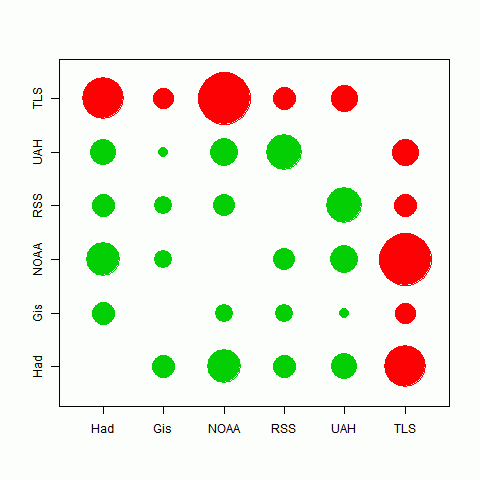
The best correlations are in fact between TempLS and HADCrut and NOAA, which likely indicates the commonality of their data sources. There is also quite good tracking between the satellite indices. It seems that the different methods used have less effect than the different data sets.

Longer periods

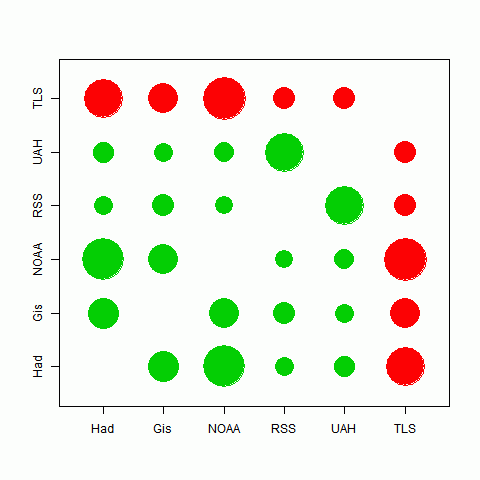
I looked at the 17 months for which TempLS made predictions. But comparisons between other indices are valid beyond that period. As indeed are comparisons with TempLS, because in calculating the monthly values I actually didn't peek.

The story is very similar. All the correlations are now highly significant. I'll just show below the circle plot for periods of five and ten years:

Correlations over 5 years	Correlations over 10 years

Correlation of TempLS and GISS seems better over the longer periods, and with NOAA not quite so good..

 

Conclusions

There are interesting patterns of correlation between the various temperature indices. Those using similar datasets correlate very well. GISS, which uses a more diverse set, behaves rather differently.

TempLS fits very well into the NOAA/HADCrut grouping.