May global surface TempLS up 0.012°C from April.

The TempLS mesh anomaly (1961-90 base) was 0.67°C in May, up from 0.658°C in April. It was cool relative to recent Mays, although 2018 and 2015 were a little cooler.. The NCEP/NCAR reanalysis base index rose more - 0.089°C. However, it did not rise much in April, when TempLS did.

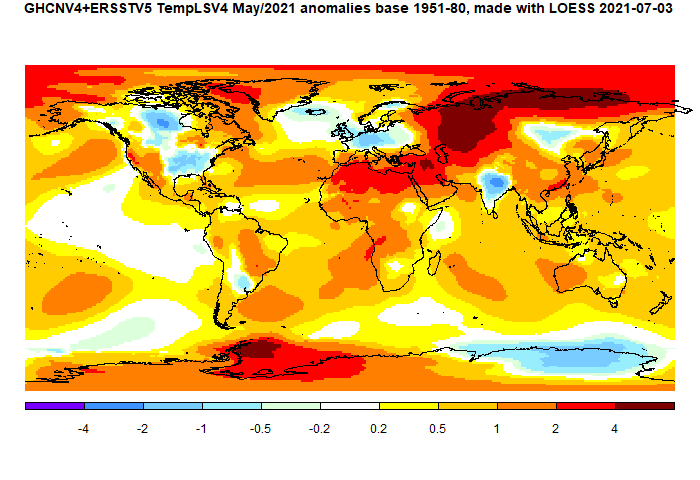
Cold patches in W Europe and Eastern US have been talked about. Also cold in India and N Canada. But it was warm in central Russia and much of the Arctic. Also in N Africa and the Middle East.

Here is the temperature map, using the LOESS-based map of anomalies.


 

As always, the 3D globe map gives better detail.

This post is part of a series that has now run since 2011. The TempLS mesh data is reported here, and the recent history of monthly readings is here. Unadjusted GHCN is normally used, but if you click the TempLS button there, it will show data with adjusted, and also with different integration methods. There is an interactive graph using 1981-2010 base period here which you can use to show different periods, or compare with other indices. There is a general guide to TempLS here.

The reporting cycle starts with a report of the daily reanalysis index on about the 4th of the month. The next post is this, the TempLS report, usually about the 8th. Then when the GISS result comes out, usually about the 15th, I discuss it and compare with TempLS. The TempLS graph uses a spherical harmonics to the TempLS mesh residuals; the residuals are displayed more directly using a triangular grid in a better resolved WebGL plot here.

A list of earlier monthly reports of each series in date order is here:

1. NCEP/NCAR Reanalysis report
2. TempLS report
3. GISS report and comparison with TempLS