Mathematics of FEM/LOESS
It's actually a true hybrid of the finite element method (FEM) and LOESS (locally estimated scatterplot smoothing). In LOESS a model is fitted locally by regression, usually to get a central value. In FEM/LOESS, the following least squares parameter fit is made:The standard FEM approximate function is f(z)=ΣaᵢBᵢ(z) where z is location on the sphere, B are the basis functions described in the previous post, and aᵢ are the set of coefficients to be found by fitting to a set of observations that I will call y(z). The LS target is
SS=∫(f(z)-y(z))^2 dz
This has to be estimated knowing y at a discrete points (stations). In FEM style, the integral is split into integrals over elements, and then within elements the integrand is estimated as mean (f(zₖ)-y(zₖ))^2 over points k. One might question whether the sum within elements should be weighted, but the idea is that the fitted f() takes out the systematic variation, so the residuals should be homogeneous, and a uniform mean is correct.
So differentiating wrt a to minimise:
∫(f(z)-y(z))Bᵢ(z) dz = 0
Discretising:
Σₘ Eₘ (ΣₖBᵢ(zₖ)Bₙ(zₖ)aₙ)/(Σₖ1) = Σₘ Eₘ (ΣₖBᵢ(zₖ)yₖ)/(Σₖ1)
The first summation is over elements, and E are their areas. In FEM style, the summations that follow are specific to each element, and for each E include just the points zₖ within that element, and so the basis functions in the sum are those that have a node within or on the boundary if that element. The denominators Σₖ1 are just the count of points within each element. It looks complicated but putting it together is just the standard FEM step of assembling a mass matrix.
In symbols,this is the regression equation
H a = B* w B a = B* w y
where B is the matrix of basis functions evaluated at zₖ, B* transpose, diagonal matrix w the weights Σₘ/(Σₖ1) (area/count), y the vector of readings, and a the vector of unknown coefficients.
To integrate a specific y, this has to be solved for a:
a=H-1B* w y
and then ΣaᵢBᵢ(z) integrated on the globe
Int = ΣaᵢIᵢ where Iᵢ is the integral of function Bᵢ,
H is generally positive definite and sparse, so the inversion is done with conjugate gradients, using the diagonal as preconditioner.
For TempLS I need not an integral but weights. So I have to calculate
wt = I H-1B* w
It sounds hard, but it is a well trodden FEM task, and is computationally quite fast. In all this a small multiple of a Laplacian matrix is added to H to ensure corresponding infilling of empty or inadequately constrained cells.
Comparisons
I ran TempLS using the FEM/LOESS weighting with 9 modes, h2p2, h2p3, h2p4,...h43,h4p4. I calculated the RMS of differences between monthly averages, pairwise, for the years 1900-2019, and similar differences between and within the advanced methods MESH, LOESS and INFILL (see here for discussion, and explanation of the h..p.. notation). Here is a table of results, of RMS difference in °C, multiplied by 1000:| MESH | LOESS | INFILL | h2p2 | h3p2 | h4p2 | h5p2 | h2p3 | h3p3 | h4p3 | h5p3 | h2p4 | h3p4 | h4p4 | h5p4 | h2p5 | h3p5 | h4p5 | h5p5 | |
| MESH | 0 | 18 | 19 | 26 | 20 | 19 | 19 | 21 | 18 | 17 | 19 | 18 | 17 | 17 | 19 | 19 | 19 | 19 | 22 |
| LOESS | 18 | 0 | 25 | 24 | 22 | 19 | 22 | 20 | 22 | 20 | 23 | 19 | 22 | 21 | 24 | 22 | 23 | 24 | 27 |
| INFILL | 19 | 25 | 0 | 27 | 19 | 17 | 14 | 21 | 14 | 13 | 11 | 17 | 11 | 11 | 10 | 14 | 11 | 10 | 12 |
| h2p2 | 26 | 24 | 27 | 0 | 24 | 25 | 26 | 21 | 24 | 24 | 26 | 22 | 25 | 25 | 26 | 26 | 26 | 27 | 28 |
| h3p2 | 20 | 22 | 19 | 24 | 0 | 17 | 16 | 16 | 11 | 16 | 17 | 16 | 12 | 17 | 18 | 16 | 17 | 17 | 21 |
| h4p2 | 19 | 19 | 17 | 25 | 17 | 0 | 14 | 15 | 12 | 8 | 16 | 12 | 13 | 10 | 14 | 14 | 16 | 17 | 20 |
| h5p2 | 19 | 22 | 14 | 26 | 16 | 14 | 0 | 17 | 11 | 11 | 6 | 13 | 10 | 10 | 12 | 0 | 6 | 8 | 12 |
| h2p3 | 21 | 20 | 21 | 21 | 16 | 15 | 17 | 0 | 16 | 16 | 19 | 10 | 17 | 17 | 19 | 17 | 19 | 20 | 23 |
| h3p3 | 18 | 22 | 14 | 24 | 11 | 12 | 11 | 16 | 0 | 10 | 11 | 12 | 6 | 10 | 12 | 11 | 11 | 13 | 16 |
| h4p3 | 17 | 20 | 13 | 24 | 16 | 8 | 11 | 16 | 10 | 0 | 11 | 11 | 9 | 4 | 9 | 11 | 11 | 12 | 16 |
| h5p3 | 19 | 23 | 11 | 26 | 17 | 16 | 6 | 19 | 11 | 11 | 0 | 15 | 9 | 9 | 10 | 6 | 0 | 4 | 8 |
| h2p4 | 18 | 19 | 17 | 22 | 16 | 12 | 13 | 10 | 12 | 11 | 15 | 0 | 13 | 12 | 15 | 13 | 15 | 16 | 20 |
| h3p4 | 17 | 22 | 11 | 25 | 12 | 13 | 10 | 17 | 6 | 9 | 9 | 13 | 0 | 8 | 10 | 10 | 9 | 10 | 14 |
| h4p4 | 17 | 21 | 11 | 25 | 17 | 10 | 10 | 17 | 10 | 4 | 9 | 12 | 8 | 0 | 6 | 10 | 9 | 10 | 14 |
| h5p4 | 19 | 24 | 10 | 26 | 18 | 14 | 12 | 19 | 12 | 9 | 10 | 15 | 10 | 6 | 0 | 12 | 10 | 9 | 12 |
| h2p5 | 19 | 22 | 14 | 26 | 16 | 14 | 0 | 17 | 11 | 11 | 6 | 13 | 10 | 10 | 12 | 0 | 6 | 8 | 12 |
| h3p5 | 19 | 23 | 11 | 26 | 17 | 16 | 6 | 19 | 11 | 11 | 0 | 15 | 9 | 9 | 10 | 6 | 0 | 4 | 8 |
| h4p5 | 19 | 24 | 10 | 27 | 17 | 17 | 8 | 20 | 13 | 12 | 4 | 16 | 10 | 10 | 9 | 8 | 4 | 0 | 6 |
| h5p5 | 22 | 27 | 12 | 28 | 21 | 20 | 12 | 23 | 16 | 16 | 8 | 20 | 14 | 14 | 12 | 12 | 8 | 6 | 0 |
The best agreement between the older methods is between MESH and LOESS at 18. Agreement between the higher order FEM results is much better. Agreement of FEM with MESH is a little better, with LOESS a little worse. The agreement with INFILL is better again, but needs to be discounted somewhat. The reason is that in earlier years there is a large S Pole region without data. Both INFILL and FEM deal with this with Laplace interpolation, so I think that spuriously enhances the agreement.
As will be seen later, there is a change in the matchings at about 1960, when Antarctic data becomes available. So I did a similar table just for the years since 1960:
| MESH | LOESS | INFILL | h2p2 | h3p2 | h4p2 | h5p2 | h2p3 | h3p3 | h4p3 | h5p3 | h2p4 | h3p4 | h4p4 | h5p4 | h2p5 | h3p5 | h4p5 | h5p5 | |
| MESH | 0 | 11 | 11 | 23 | 17 | 16 | 14 | 18 | 13 | 12 | 12 | 15 | 12 | 11 | 10 | 14 | 12 | 12 | 16 |
| LOESS | 11 | 0 | 10 | 19 | 14 | 12 | 10 | 14 | 10 | 9 | 9 | 10 | 9 | 8 | 9 | 10 | 9 | 10 | 14 |
| INFILL | 11 | 10 | 0 | 21 | 16 | 16 | 13 | 17 | 13 | 12 | 11 | 15 | 11 | 10 | 9 | 13 | 11 | 10 | 13 |
| h2p2 | 23 | 19 | 21 | 0 | 20 | 20 | 20 | 18 | 20 | 20 | 20 | 18 | 20 | 20 | 21 | 20 | 20 | 20 | 22 |
| h3p2 | 17 | 14 | 16 | 20 | 0 | 15 | 15 | 13 | 10 | 14 | 15 | 13 | 11 | 14 | 16 | 15 | 15 | 15 | 19 |
| h4p2 | 16 | 12 | 16 | 20 | 15 | 0 | 12 | 12 | 10 | 7 | 14 | 9 | 10 | 9 | 13 | 12 | 14 | 16 | 20 |
| h5p2 | 14 | 10 | 13 | 20 | 15 | 12 | 0 | 15 | 11 | 9 | 6 | 11 | 10 | 10 | 11 | 0 | 6 | 8 | 13 |
| h2p3 | 18 | 14 | 17 | 18 | 13 | 12 | 15 | 0 | 12 | 13 | 16 | 10 | 13 | 14 | 16 | 15 | 16 | 17 | 20 |
| h3p3 | 13 | 10 | 13 | 20 | 10 | 10 | 11 | 12 | 0 | 9 | 12 | 8 | 6 | 9 | 11 | 11 | 12 | 13 | 17 |
| h4p3 | 12 | 9 | 12 | 20 | 14 | 7 | 9 | 13 | 9 | 0 | 10 | 9 | 7 | 4 | 8 | 9 | 10 | 11 | 16 |
| h5p3 | 12 | 9 | 11 | 20 | 15 | 14 | 6 | 16 | 12 | 10 | 0 | 13 | 9 | 9 | 9 | 6 | 0 | 4 | 9 |
| h2p4 | 15 | 10 | 15 | 18 | 13 | 9 | 11 | 10 | 8 | 9 | 13 | 0 | 9 | 9 | 12 | 11 | 13 | 14 | 18 |
| h3p4 | 12 | 9 | 11 | 20 | 11 | 10 | 10 | 13 | 6 | 7 | 9 | 9 | 0 | 7 | 9 | 10 | 9 | 11 | 15 |
| h4p4 | 11 | 8 | 10 | 20 | 14 | 9 | 10 | 14 | 9 | 4 | 9 | 9 | 7 | 0 | 6 | 10 | 9 | 10 | 15 |
| h5p4 | 10 | 9 | 9 | 21 | 16 | 13 | 11 | 16 | 11 | 8 | 9 | 12 | 9 | 6 | 0 | 11 | 9 | 9 | 13 |
| h2p5 | 14 | 10 | 13 | 20 | 15 | 12 | 0 | 15 | 11 | 9 | 6 | 11 | 10 | 10 | 11 | 0 | 6 | 8 | 13 |
| h3p5 | 12 | 9 | 11 | 20 | 15 | 14 | 6 | 16 | 12 | 10 | 0 | 13 | 9 | 9 | 9 | 6 | 0 | 4 | 9 |
| h4p5 | 12 | 10 | 10 | 20 | 15 | 16 | 8 | 17 | 13 | 11 | 4 | 14 | 11 | 10 | 9 | 8 | 4 | 0 | 7 |
| h5p5 | 16 | 14 | 13 | 22 | 19 | 20 | 13 | 20 | 17 | 16 | 9 | 18 | 15 | 15 | 13 | 13 | 9 | 7 | 0 |
Clearly the agreement is much better. The best of the older methods is between LOESS and INFILL at 10. But agreement between high order FEM methods is better. Now it is LOESS that agrees well with FEM - better than the others. Of course in assessing agreement, we don't know which is right. It is possible that FEM is the best, but not sure.
Here are some time series graphs. I'll show a time series graph first, but the solutions are too close to distinguish much.
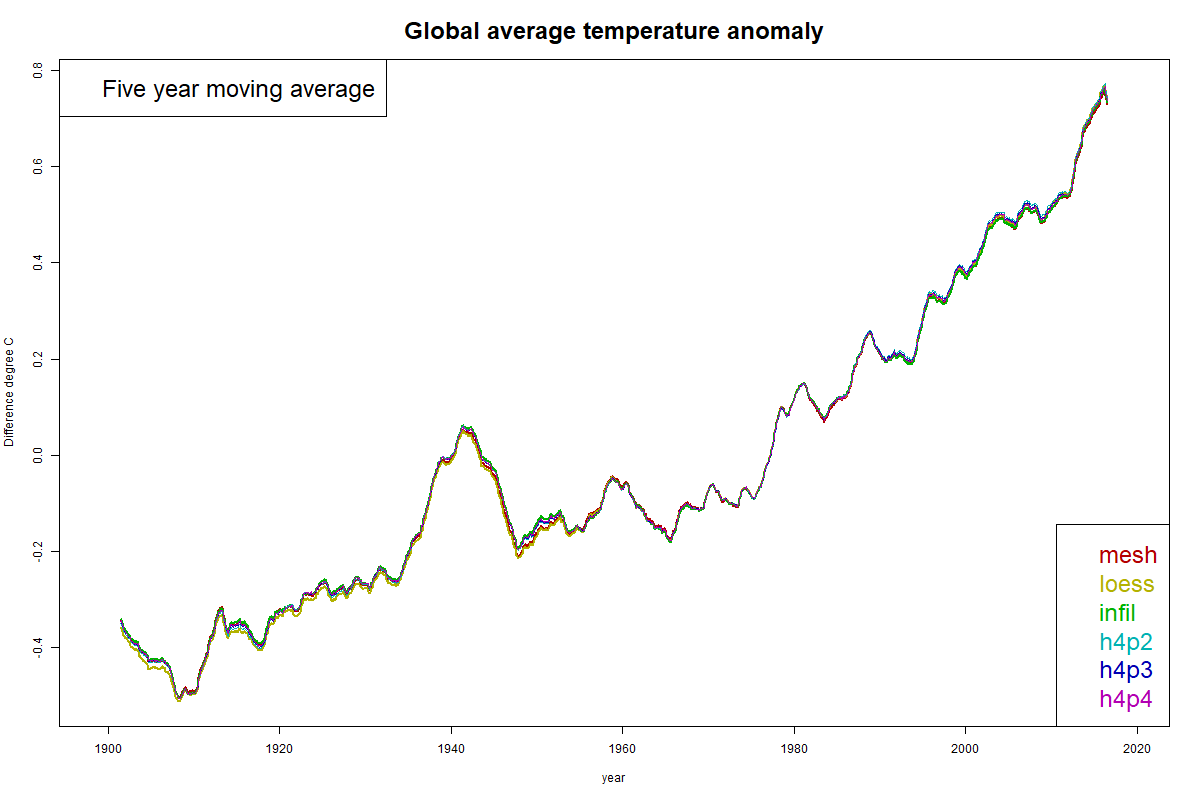
Difference plots are more informative. These are made by subtracting one of the solutions from the others. I have made plots using each of MESH, LOESS and INFILL as reference. You can click the buttons below the plot to cycle through.
There is a region of notably good agreement between 1960 and 1990. This is artificial, because that is the anomaly base period, so all plots have mean zero there. Still, they are unusually aligned in slope.
Before 1960, LOESS deviates from the FEM curves, MESH less, and INFILL least. The agreement of INFILL probably comes from the common use of Laplace interpolation for the empty Antarctic region. In the post 1990 period, it is LOESS which best tracks with FEM.
However, I should note that no discrepancies exceed about 0.02°C.












Hum, it seems that the discrepancy might be related to some artifact in the 1940's. Maybe you have discovered a test to pinpoint anomalous data here.
ReplyDeleteThe issue with the 1940's is that the corrections are abrupt, drawn along the war-year endpoints when measurement techniques changed dramatically. Differing filtering techniques will either exaggerate or suppress the adjustments made at the boundary years. A high-pass filter will enhance, while a low-pass will suppress. BTW, the strongest multiple El Nino peak also occurred in the early 1940's making it eve more difficult to adjust.
ReplyDeleteI think I understand your new method . It has got me interested again in the use of icosahedral grids (FEM) for the earth's surface. You seem to be using what I call a level 4 Icosahedral grid with 2562 nodes, then using LOESS to fit the station values to a polynomial for each triangle. The result are nice smooth anomaly distributions. Do you also interpolate into empty triangles?
ReplyDeleteI have instead been using a brute force method by stepping up to a level 5 icosahedral grid with 10224 nodes and then averaging all temperatures within the 4 times smaller triangles. Perhaps I should be using R !
Clive,
Delete"You seem to be using what I call a level 4 Icosahedral grid with 2562 nodes"
You tend to work in terms of iterated bisecting; I do fractional divisions. Each triangle is divided into n² elements. So h2 has 80 elements in total (42 nodes); h3 has 180 (92), h4 has 320 (162). So a lot fewer elements.
"Do you also interpolate into empty triangles?"
With higher order polynomials, it's harder, but there is a good solution. You need enough nodes (not just 1) to get a unique fit. The solution is using the Laplace operator. Here is how I do it for the simpler grid infill method. You have a whole lot of grid equations
NᵢTᵢ=yᵢ
where N is the number of nodes in a tri i, T is the average anomaly, and y is the sum of anomalies. It's a system of equations but may be singular if some Nᵢ=0.
Embed it in a matrix system
AᵢₖTₖ=yᵢ
(summing over k - summation convention) where A is a diagobal matrix with N's on the diag.
Let B be a Laplacian matrix. Good enough is for BT=0 to say that each cell value is the average if its neighbors - ie 3 on the diagonal (triangle grid), 0 elsewhere except, for each row, a value of -1 at each neighbor col.
Then solve (A+εB)T = y
ε needs to be large enough to make A+εB not too ill-conditioned, but small enough not to do too much smoothing of the known data. There is a lot of room there.
My new method uses sparse matrix structures and conjugate gradient methods for solving that last equation. With the FEM version, A is like a mass matrix. It's the matrix for the local regression.