The overall pattern was similar to that in TempLS. Warm in most of N America, and equally warm in Europe, especially around the Baltic. Warm in East Asia, especially Siberia. Antarctica mostly warm. Still a pattern of warm patches along about 40°S.
As usual here, I will compare the GISS and previous TempLS plots below the jump.
Here is GISS
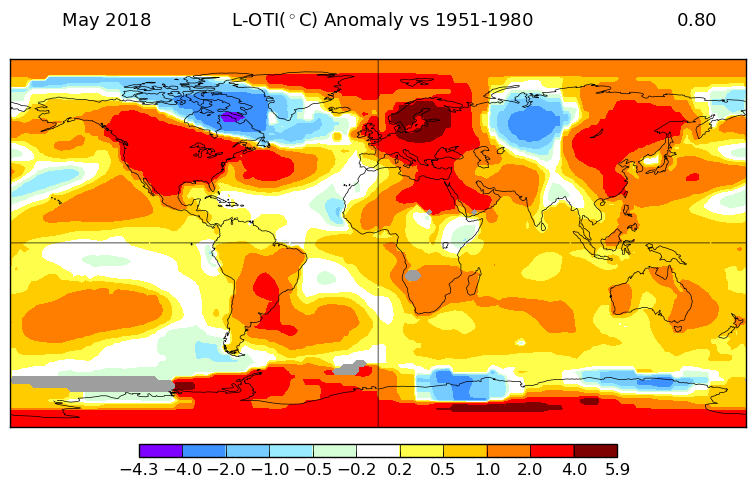
And here is the TempLS spherical harmonics plot
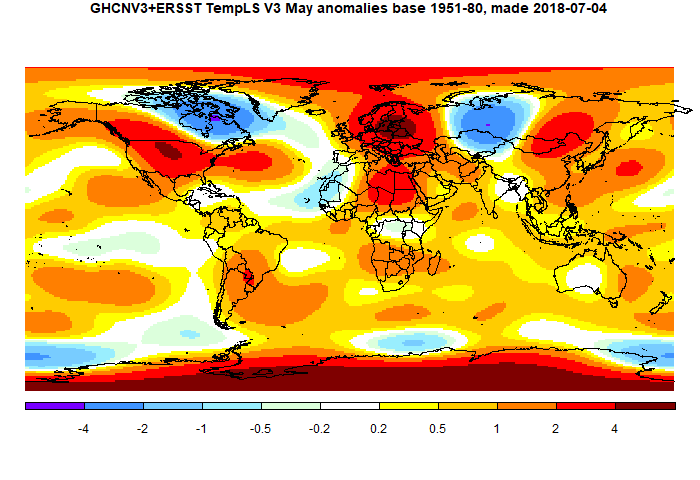
This post is part of a series that has now run for six years. The GISS data completes the month cycle, and is compared with the TempLS result and map. GISS lists its reports here, and I post the monthly averages here.
The TempLS mesh data is reported here, and the recent history of monthly readings is here. Unadjusted GHCN is normally used, but if you click the TempLS button there, it will show data with adjusted, and also with different integration methods. There is an interactive graph using 1981-2010 base period here which you can use to show different periods, or compare with other indices. There is a general guide to TempLS here.
The reporting cycle starts with a report of the daily reanalysis index on about the 4th of the month. The next post is this, the TempLS report, usually about the 8th. Then when the GISS result comes out, usually about the 15th, I discuss it and compare with TempLS. The TempLS graph uses a spherical harmonics to the TempLS mesh residuals; the residuals are displayed more directly using a triangular grid in a better resolved WebGL plot here.
A list of earlier monthly reports of each series in date order is here:
The TempLS mesh data is reported here, and the recent history of monthly readings is here. Unadjusted GHCN is normally used, but if you click the TempLS button there, it will show data with adjusted, and also with different integration methods. There is an interactive graph using 1981-2010 base period here which you can use to show different periods, or compare with other indices. There is a general guide to TempLS here.
The reporting cycle starts with a report of the daily reanalysis index on about the 4th of the month. The next post is this, the TempLS report, usually about the 8th. Then when the GISS result comes out, usually about the 15th, I discuss it and compare with TempLS. The TempLS graph uses a spherical harmonics to the TempLS mesh residuals; the residuals are displayed more directly using a triangular grid in a better resolved WebGL plot here.
A list of earlier monthly reports of each series in date order is here:












They are getting close to understanding tropical oscillations in this paper
ReplyDelete"Order Out of Chaos: Slowly Reversing Mean Flows Emerge from Turbulently Generated Internal Waves"
in the prestigious Physical Review Letters! DOI: 10.1103/PhysRevLett.120.244505
The big sea change in the understanding of natural global temperature variations is that large scale behaviors are not chaotic. In the above PRL paper
Delete"An outstanding question in fluid dynamics is whether large-scale flows can be accurately captured in reduced models that do not resolve fluid motions on small spatiotemporal scales. Reduced models are necessary in many fields of fluid mechanics, since fluid phenomena often occur on a wide range of spatial and temporal scales, preventing exploration via direct numerical simulations (DNSs) of the Navier-Stokes equations."
In a previous PRL paper, "Geophysical Turbulence and the Duality of the Energy Flow Across Scales", DOI:10.1103/PhysRevLett.111.234501
"Such flows are neither 3D nor 2D, since at small scales 3D eddies may prevail. Considering the system dimensionality DS proved essential when examining critical phenomena which simplify in higher dimensions, due to more mode interactions as DS grows. Fluid turbulence is vastly different in two or three dimensions, because of the strong constraint imposed by the new 2D invariants (such as the integrated powers of vorticity). This leads to energy flowing towards the largest scales, ending up in a condensate [7]; it can take the form of features such as jets, observed in the atmosphere of planets, or in the oceans as striations [8]. Thus, geophysical turbulence is anisotropic, quasi-2D at large scale and quasi-3D at small scale [9]"
This will make our denier friend David Young very angry.
And this one:
DeleteSingularity of Navier-Stokes Equations http://arxiv.org/abs/1805.12053
"The physics of transition of a smooth laminar flow to turbulence still poses a great challenge in physics. In this study, the singularity of Navier-Stokes equations is discovered through the derivation of the Navier-Stokes equations and the analysis of the velocity profile. This is for the first time that the singularity is found where the velocity is zero. It is the inflection point on the velocity profile that leads to the discontinuity and the instability. This singularity is the origin of the spanwise vortex and the genesis of the vortex head of the hairpin vortex formed afterwards. The singularity of the Navier-Stokes equations is the cause of turbulent transition and the inherent mechanism of sustenance of fully developed turbulence.
...
From the present study, it is clear that turbulence cannot be duplicated due to the singularity of Navier-Stokes equations at a velocity inflection point and that the turbulence is composed of numerous singularities. This may be useful information for the question in the millennium prize problems"
I'm not sure that any of this says that large scale fluid flows are not chaotic. Certainly the last is just about transition to turbulence, which is chaotic. Pouquet et al are talking about how geo flows have 2D and 3D aspects, where turbulent energy cascades in opposite directions. But that is still chaotic, as indicated by the fact that DNS won't work.
DeleteConsider standing waves such as occurs with ENSO, QBO and other climate dipole behaviors. The spatial aspect of the standing wave cannot be chaotic, otherwise the position of the modes will move around. The temporal aspect of the standing wave may appear chaotic, but there are arguments that forcing will neutralize the chaotic elements.
DeleteFor example, from Osipov, Grigory V, Jürgen Kurths, and Changsong Zhou. Synchronization in Oscillatory Networks. Springer, 2007.
"Periodic external force acting on a chaotic system can destroy chaos and as a result a periodic regime appears. This effect occurs for a relatively strong forcing as well."
The recent papers are reinforcing the idea that order forms at the larger scales, despite turbulence and chaos at the lower scales.
The DNS results from GCMs consistently find a strong biennial cycle, which may be a bifurcation towards chaos, but is not chaotic.