Electronic circuit climate analogues - amplifiers and nonlinearity

This post is a follow-up to my previous post on feedback. The main message in that post was that, although talking of electronic analogues of climate feedback is popular in some quarters, it doesn't add anything mathematically. Feedback talk is just a roundabout way of thinking about linear equations.

Despite that, in this post I do want to talk more about electronic analogues. But it isn't much about feedback. It is about the other vital part of a feedback circuit - the amplifier, and what that could mean in a climate context. It is of some importance, since it is a basic part of the greenhouse effect.

The simplest feedback diagram (see Wiki) has three elements:



They are the amplifier, with gain A_OL, a feedback link, with feedback fraction β, and an adder, shown here with a minus sign. The adder is actually a non-trivial element, because you have to add the feedback to the input without one overriding the other. In the electronic system, this generally means adding currents. Adding voltages is harder to think of directly. However, the block diagram seems to express gain of just one quantity, often thought of as temperature.

In the climate analogue, temperature is usually related to voltage, and flux to current. So there is the same issue, that fluxes naturally add, but temperature is the variable that people want to talk about. As mentioned last post, I often find myself arguing with electrical engineers who have trouble with the notion of an input current turning into an output voltage (it's called a transimpedance amplifier).

If you want to use electronic devices as an analogue of climate, I think a fuller picture of an amplifier is needed. People now tend to show circuits using op amps. These are elaborately manufactured devices, with much internal feedback to achieve high linearity. They are differential, so the operating point (see below) can be zero. I think it is much more instructive to look at the more primitive devices - valves, junction transistors, FETs etc. But importantly, we need a fuller model which considers both variables, voltage and current. The right framework here is the two port network.

I've reached an awkward stage in the text where I would like to talk simultaneously about the network framework, junction transistors, and valves. I'll have to do it sequentially, but to follow you may need to refer back and forth. A bit like a feedback loop, where each depends on the other. I'll go into some detail on transistors, because the role of the operating point, fluctuations and linearity, and setting the operating point are well documented, and a good illustration of the two port treatment. Then I'll talk about thermionic valves as a closer analogue of climate.

Two Port Network

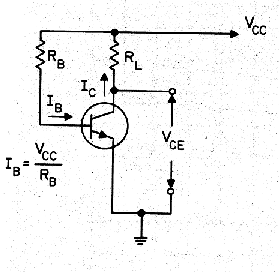
Wiki gives this diagram:


As often, engineer descriptions greatly complicate some simple maths. Many devices can be cast as a TPN, but all it means is that you have four variables, and the device enforces two relations between them. If these are smooth and can be linearised, you can write the relation for small increments y as



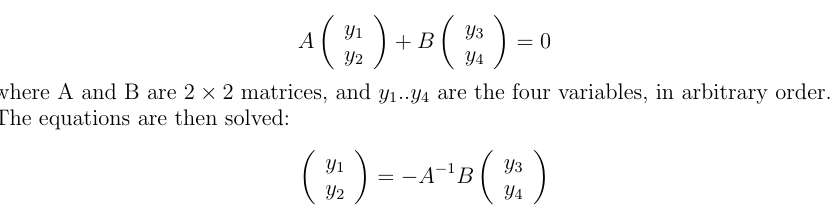
Wiki, like most engineering sources, lists many ways you could choose the variables for left and right. For many devices, some coefficients are small, so you will want to be sure that A is not close to singular. I'll show how this works out for junction transistors.

This rather general formulation doesn't treat the input and output variables separately. You can have any combination you like (subject to invertible A). For linearity, the variables will generally denote small fluctuations; the importance of this will appear in the next section.

The external circuitry will contribute extra linear equations. For example, a load resistor R across the output will add an Ohm's Law, V₂ = I₂R. Other arrangements could provide a feedback equation. With one extra relation, there is then just one free variable. Fix one, say an input, and everything else is determined.

Junction transistors

I'm showing the use of a junction transistor as amplifier because it is a well documented example of:

• a non-linear device which has a design point about which fluctuations are fairly linear
• a degree of degeneracy, in that it is dominated by a strong association between I₁ and I₂, with less dependence on V₂ and little variation in V₁. IOW, it is like a current amplifier, with amplification factor β.
• there is simple circuitry that can stably establish the operating point.

Here from Wiki, is a diagram of a design curve, which is a representation of the two-port relation. It takes advantage of the fact that there is a second relation which is basically between I₁ and V₁, with V₁ restricted to a narrow range (about 0.6V for silicon).



The top corner shows the transistor with variables labelled; the three pins are emitter E, base B and collector C. In TPN terms, I₁ is the base current I_B; I₂ is the current from collector to emitter I_C, and V₂ is the collector to emitter voltage V_CE. The curves relate V₂ and I₂ for various levels of I₁. Because they level off, the dependence is mainly between I_C and I_B. The load line in heavy black shows the effect of connecting the collector via a load resistor. This constrains V₂ and I₂ to lie on that line, and so both vary fairly linearly with I₁.

The following diagrams have real numbers and come from my GE transistor manual, 1964 edition, for a 2N 1613 NPN transistor. The left is a version of the design curves diagrammed above, but with real numbers. It shows as wavy lines a signal of varying amplitude as it might be presented as base current (top right) and appear as a collector voltage (below). The load resistor line also lets you place it on the y axis, where you can see the effect of current amplification, by a factor of about 100. The principal purpose of these curves is to show how non-linearity is expressed as signal clipping.





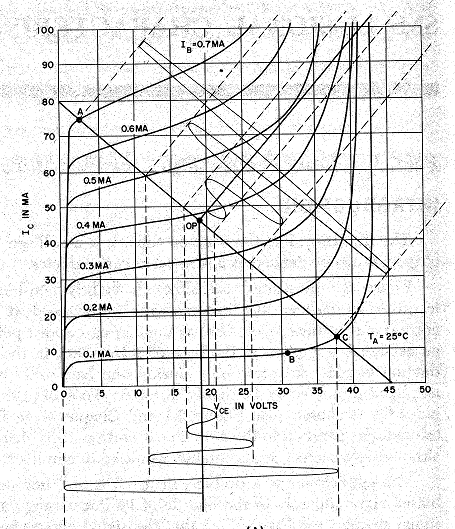
I have included the circuit on the right, a bias circuit, to show how the design operating point is achieved. The top rail is the power supply, and since the base voltage is near fixed at about 0,6V, the resistor R_B determines the base current curve. The load R_L determines the load line, so where these intersect is the operating point.

So let's see how this works out in the two-port formulation. We have to solve for two variables; the choice is the hybrid or h- parameters:



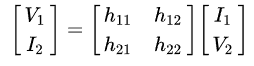
Hybrid suggests the odd combination; input voltage V₁ and output current I₂ are solved in terms of input current I₁ and output voltage V₂. The reason is that the coefficients are small, except for h₂₁ (also β). There is some degeneracy; there isn't much dependence at all on V₂, and V₂ is then not going to vary much.So these belong on the sides they are placed. I₂ and I₁ could be switched; that is called inverse hybrid (g-). I've used the transistor here partly as a clear example of degeneracy (we'll see more).

Thermionic valve and climate analogue

From Wiki comes a diagram of a triode



The elements are a heated cathode k in a vacuum tube, which can emit electrons, and an anode a, at positive voltage, to which they will move, depending on voltage. This current can be modulated by varying the voltage applied to the control grid g, which sits fairly close to the cathode.

I propose the triode here because it seems to me to be a closer analogue of GHGs in the atmosphere. EE's sometimes say that the circuit analogue of climate fails because they can't see a power supply. That is because they are used to fixed voltage supplies. But a current supply works too, and that can be seen with the triode. A current flows and the grid modulates it, appearing to vary the resistance. A FET is a more modern analogue, in the same way. And that is what happens in the atmosphere. There is a large solar flux, averaging about 240 W/m² passing through from surface to TOA, much of it as IR. GHGs modulate that flux.

A different two-port form is appropriate here. I₁ is negligible, so should not be on the right side. Inverse hyprid could be used, or admittance. It doesn't really matter which, since the outputs are likely to be related via a load resistor.

Climate amplifier

So thinking more about the amplifier in the climate analogue, first as a two port network. Appropriate variables would be V₁,I₁ as temperature and heat flux at TOA, and V₂, I₂ as temperature, upward heat flux at the surface. V₂ is regarded as an output, and so should be on the LHS, and I₁ as an input, on the right. One consideration is that I₂ is constrained as being the fairly constant solar flux at the surface, so it should be on the RHS. That puts V₁ on the left and pretty much leads to an impedance parameters formulation - a two variable form of Ohm's Law.

The one number we have here is the Planck parameter, which gives the sensitivity before feedback of V₂ to I₁ (or vice versa). People often think that this is determined by the Stefan-Boltzmann relation, and that does give a reasonably close number. But in fact it has to be worked out by modelling, as Soden and Held explain. Their number comes to about 3.2 Wm⁻²/K. This is a diagonal element in the two port impedance matrix, and is treated as the open loop gain of the amplifier. But the role of possible variation of the surface flux coefficient should alos be considered.

As my earlier post contended, mathematically at least, feedback is much less complicated than people think. The message of this post is that if you want to use circuit analogues of climate, a more interesting question is, how does the amplifier work?