GWPF's "statistical forecast"

There was a flurry of articles in the usual Press places, about a statistical forecast of future temperatures sponsored by the GWPF (Murdoch, Express,Daily Mail). Blog reaction tended to focus on the total ignoring of physics, or, more frequently, the observation that:
"The GWPF paid Terence Mills, professor of applied statistics at Loughborough University, £3,000 to write the report."

Well, those are cogent criticisms. But time series analysis is a respectable enough endeavour, so I read the report to see if the GWPF got its money's worth.

The answer is no, or maybe from their poiunt of view, yes. There are about 33 quite well-written pages, borrowing I suspect from lecture notes (nothing wrong with that). But the forecasts themselves are worthless. Gavin Schmidt tweeted the following test of the HADCRUT forecasts, which were from 2014, after just one year:

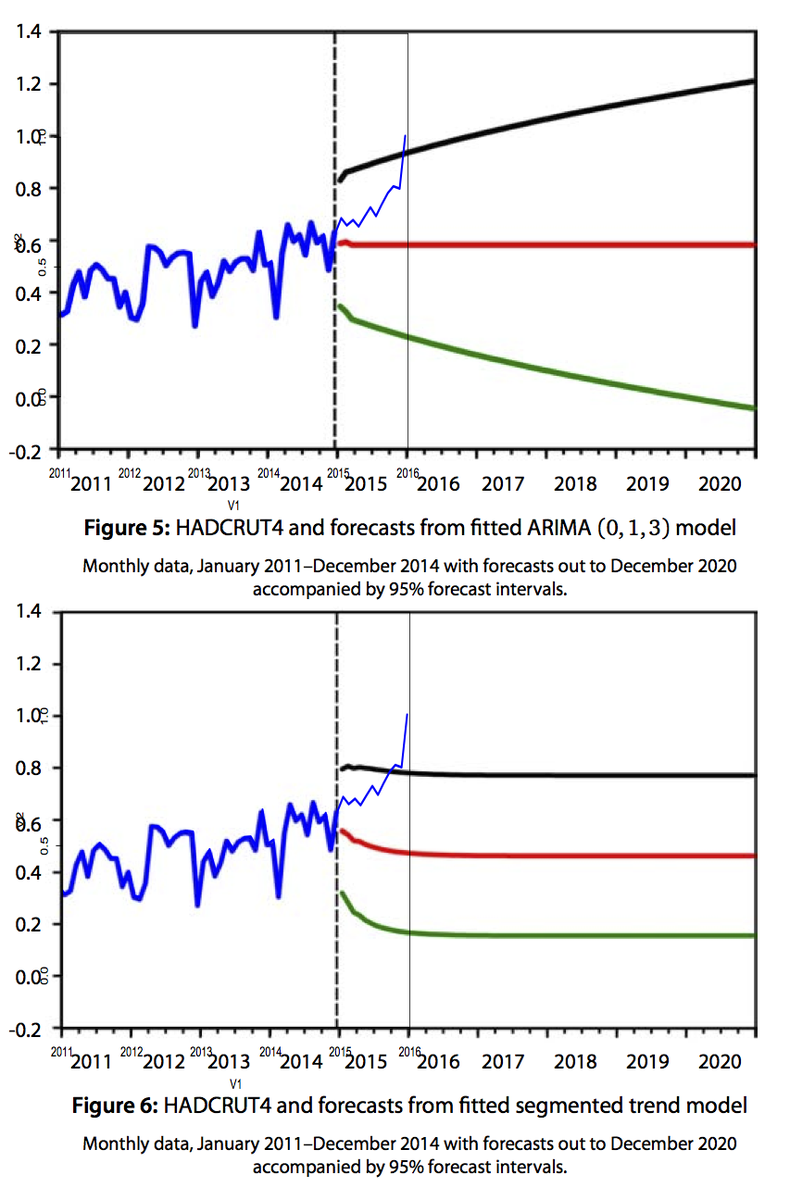
The thin blue line is 2015 information added by Gavin, and as you see, they are already outside the confidence intervals.

Now it might be said that briefly going beyond the CI's is note a complete refutation, though it very likely won't be brief. The real reason that the forecasts are worthless is that in every case they simply foretell that the expectation for the future is no change at all. The forecast is just constant after a few months, based on a very recent weighted average of data points. It has to be - that is built into the models. In fact, the author actually says this:
"The central aim of this report is to emphasise that, while statistical forecasting appears highly applicable to climate data, the choice of which stochastic model to fit to an observed time series largely determines the properties of forecasts of future observations and of measures of the associated forecast uncertainty, particularly as the forecast horizon increases."
It would be good if he had emphasised that more; it's true (my bold). But in fact what is emphasised is the forecast. And in the press, the slow growth of the forecast. But, as said, that is built in. His models are simply incapable of forecasting change. I'll show why.

You can see from the time series plot of HADCRUT 4:

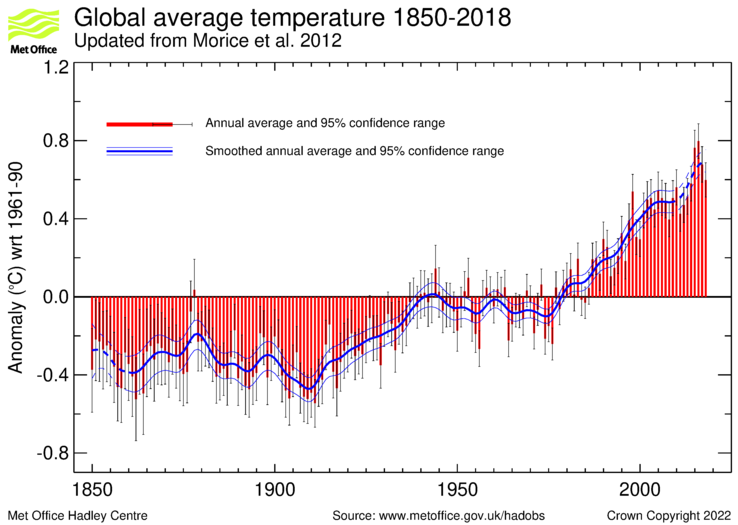
that especially over the last fifty years, forecasting on the basis of nothing changing would have been very unsuccessful. And there is no reason to expect it to be better in the future. So what gives?

Mills does two HADCRUT forecasts, as shown in Gavin's annotated plot above. One is a fit to the whole period, and one is a piecewise fit, in segments of which the last starts in 2002 (diagram below). For the whole period fit, he chooses a ARIMA(0,1,3) model:



The a_t terms are iid random variables with the stated σ. I see no benefit in the extra complexity, but that is what he did. Now the key is the words "Omitting this from the model...". The constant term (drift) 0.0005 is the term that provides the trend. It is about 0.6 °C/Century - about what most people find for trend since 1850. And if you use just about any linear regression model, it will say that the trend is highly significant. I got a t-value, with AR(1), of 51. Yet he says it is not significant, and sets it to zero. And it is that setting to zero which guarantees a zero trend of the prediction. If he had left it at 0.6 °C/century, that would have been the predicted future trend. He could have set it to 1.2; that is at least as likely as zero.

So why does he get such little significance? The reason is that he differences, and then allows a different distribution (ARIMA) for the residuals. When summed again, the errors are now modelled as a random walk (with ARIMA modelled steps), as he explains. And it is far easier for a random walk to emulate a trend. His model has far less ability to discriminate trend value.

There are two things badly wrong with this:

1. A random walk is unbounded, and is unphysical. Over time, temperatures can go anywhere, and will with eventual probability 1. They will surely go below 0K, and above 100°C. That hasn't happened. Now some may say, well, maybe the random walk is only for a finite period. But that is no use for prediction, if you don't know when the period is. And anyway it is highly implausible that the mechanism would suddenly change.
2. A random walk is a solution to a stochastic de. The future is determined principally by the current state. But there is no reason to think that random fluctuations of weather would behave that way. A heat wave doesn't establish a new base point. We know that there is physics that brings it back to equilibrium (eg S-B).

But what is then very bad is that, by omitting the constant, he treats it as zero with no uncertainty. So it goes into the prediction as certainly zero, even though we know it was positive.

Also bad is that he uses one model for the whole range to predict from 2014. But clearly things have changed since 1850. To remedy this, perhaps, Mills also offers a segmented model:

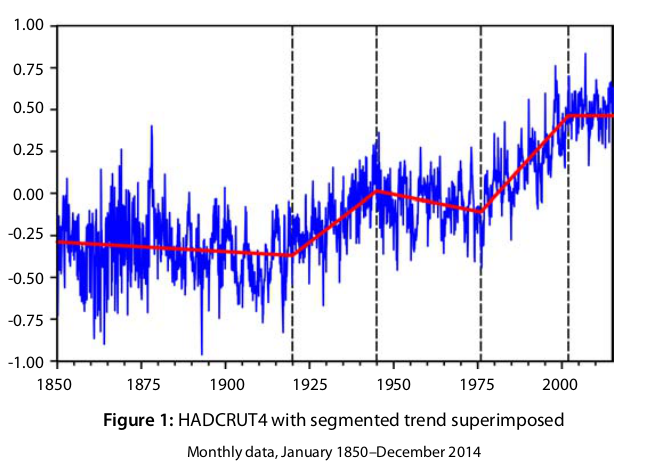
This time he uses an autoregressive model, AR(4), for the residuals of a linear regression. So at least the residuals aren't modelled as a random walk. He uses the final segment 2002-2014 for the prediction, and says of it that the slope is 0.8°C/Cen, and the t-value relative to 0 is 1.26. So again, on this basis he omits the trend term. This again has the effect of treating it as certainly zero. But because of the short interval, the trend was both positive (best estimate) and very uncertain. If he had made it the observed 0.8, this slope would have carried through to the prediction, and within the 95% limits it could have been as high as 2.0 &C/Century, which is about what GCMs predict for the next few decades.

Conclusion

I come back to what he said:
"the choice of which stochastic model to fit to an observed time series largely determines the properties of forecasts"
It does. And the trendless future is entirely determined by his decision to take the observed positive slopes and replace them with zero, with no uncertainty. This arbitrary and baseless decision is the entire basis for his no-growth forecasts. The forecast method itself is primitive - it simply projects to the future from a weighted average of a few of the most recent data points.

Update. I've been able to emulate the HADCRUT forecast process. The ARIMA forecasts, with no "omissions", are virtually identical to what you would get by projecting a straight line OLS regression slope over the same interval, shifted to start from some smoothed value of the endpoint. The only "improvement" here is that that linear extrapolation has its slope set arbitrarily to zero. I hope to blog the calculations tomorrow.