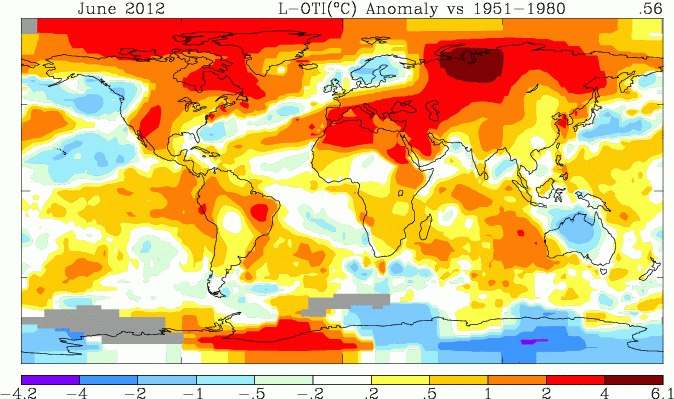
The TempLS analysis, based on GHCNV3 land temperatures and the ERSST sea temps, showed a monthly average anomaly of 0.50°C for June, down slightly from 0.52 °C in May. UAH seems to be the only other result out, showing a 0.08 C increase. There are more details at the
latest temperature data page.
I'll show here the usual spherical harmonics plot of area distribution of temperature. But I'll also show a more elaborate interactive plot of station temperatures. This gives a good guide as to what data is currently in, as well as a basis for comparing the spherical harmonics smoothing. It's the same style I showed last
November
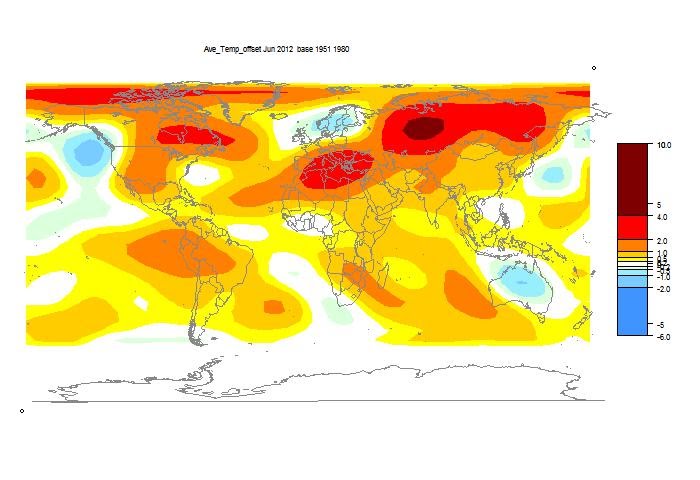
Above is the spherical harmonics plot done with the GISS colors and temperature intervals, and as usual I'll post a comparison when GISS comes out. And next is the interactive plot, with some brief usage guidance below.

|
|
How it works
The flat map at top right is your navigator. If you click a point in that, the sphere will rotate so that point appears in the centre.
The buttons below allow modification. Set what you want, and press refresh. You can show stations, and the mesh, and magnify 2×, 4×, or 8× (by setting both). You can click again to unset (and press refresh).
Then you can click in the sphere. At the bottom on the right, the nearest station name and anomaly will appear. You may want to have stations displayed here. You'll see two faint numbers next to "stations". This indicates how much your clicked missed the station by (in pixels).