A new paper by McKitrick, McIntyre and Hermann is being discussed. David Stockwell and Jeff Id have threads, and there is now one at Climate Audit and at James Annan.
An earlier much-discussed paper by Santer et al comparing models with tropical tropospheric temp observations contended that there was no significant difference between model outputs and observation. MMH say that this is an artefact of Santer using a 1979-2000 period, and if you look at the data now available, the differences are highly significant.
In discussion at the Air Vent, I've been contending that MMH underestimate variability in their significance test. They take account of the internal variability of both models and observations, so that each model and obs set has associated noise. But they do not allow for variance between models. I said that this restricts their conclusion to the particular set of model runs that they examined, and this extra variability would have to be taken into account to make statements about models in general.
However, it's clear to me now that this problem extends even to the analysis of the sample that they looked at. They list, in Table 1, the data series and their trends with standard error. The first 23 are models. In Figs 2 and 3 they show the model mean with error bars. I looked at the mid-trop (MT) set; in Table 2 they give the mean as 0.253, sd 0.012, and indeed, with error bars 0.024 that is what Fig 3 seems to show.
So I plotted Table 1 as a histogram. Here's how it showed, with the mean and error bars from Table 2 MMH marked in red.
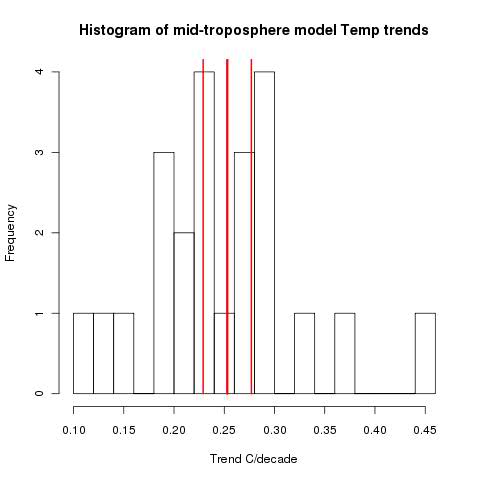
The key thing to note is what James Annan also noted. The models are far more scattered than the supposed distribution indicates. The models themselves are significantly different from the model mean.
Update: Of course, the error bars are for the mean, not the distribution. But the bars seem very tight. A simple se of the mean of the trends would be about 0.022. And that does not allow for the uncertainty of the trends themselves.
Update 2: As Deep Climate points out below, that last update figure is wrong. A corrected figure is fairly close to what is in MMH's table.
However, Steve McIntyre says that the right figure to use is the within-groups variance - some average of the se's of the trends of each model. That does seem to be the basis for their figure. I think both should be used, which would increase the bound by a factor of about sqrt(2).












I tried posting on this, the night the post went up at CA. I don't know all them fancy shtats and shtuff. But I know how to ask questions.
ReplyDeleteI said, does it make any sense to describe "the models" as predicting X plus or minus 50% trend over a century, and then here have "the models" predict a tropo trend within 10%? BTW, also for a shorter time (and with less forcing), both making natural variability more an effect.
McIntyre clipped my comment saying it had no relation to the topic.
I mean think about it! If the models do that kind of prediction as in MMH figures, than we ought to have "point estimates" (practically) for the expected increase over the century.
I'm not sure of the exact details of how each model treats solar activity, but when evaluating model output since 2000 (the start of "the future"), it's worth remembering that solar activity is treated as fixed at a time when we've gone from solar max to solar min. If the solar cycle is worth 0.1 from peak to trough, or 0.05 from "average" to trough (at the surface), then we're looking at non-negligible, temporary reductions in warming given that we are evaluating only 30 years of satellite data.
ReplyDeleteNick:
ReplyDeleteI am "on the denialist side", but I find my side making lots of mistakes and playing rhetorical games. Where can I go to find others like me. The lukewarmers don't get it done for me. Seen Lucia spend years dancing around. Seen Moshpit take WAY too long to think through things critically.
Maybe, I should just leave the climatosphere again and go back to fitness blogs? Lots of good arguments about nutrition and machines versus freeweights.
Oh scientist. Are you about to be banned again?
ReplyDeleteWhy isn't Chad using the same multi-model comparison method he used in this post?
http://treesfortheforest.wordpress.com/2010/03/04/north-american-snow-cover/
Or that Zeke used here?
http://rhinohide.wordpress.com/2010/02/27/steve-goddards-snowjob/
No. And the first time, when everyone thought I was banned and even just talked about it as accepted fact, I wasn't a bit banned. I just got disgusted with McIntyre's little dishonesties. I've seen this movie way too much. Have analyzed it in detail. And at the end of the day, who cares it's just a jerkoff on the Internet.
ReplyDeleteAnd this is all said as someone who wants the denialists to win, honest, but only if they are correct, are revealing truth, and who thinks they should show all truths they find, not just those that help their cause.
I'm headed back to lifting weights. Screw the climate jerks.
Nick it would interesting to apply your insights to the attribution tests.
ReplyDeleteNobody seems willing to even discuss that issue.
Nick,
ReplyDeleteI decided to look at LT, not MT. Of course, I've noticed the same problem you and others have.
http://deepclimate.files.wordpress.com/2010/08/lt-model-histogram.gif
http://deepclimate.files.wordpress.com/2010/08/lt-model-histogram-adj.gif
The latter shows the centre bin adjusted to exactly the MMH C.I. for LT model trend. It contains only 11 of the 57 runs.
I'll have a post with these and some other observations later on.
I've noticed a discrepancy between the table and the figures. The table has LT at 0.27 and MT at 0.25. But the figure clearly shows lower trends (0.26 and 0.24). This actually accords with the trend of the model run ensemble mean I calculated from the LT data set. (MMH uses an average of models, but each weighted by number of runs, which comes to much the same thing). Also, when I try to calculate the results for individual models (I did the first three), I get slightly lower values in general. I know I've translated to years properly, because the baseline (1979-1999) averages to zero (4 sig. figures) for each run.
You might want to check the same thing for MT.
cce,
I think solar peaked a bit later, but your point is well taken, especially since the minimum was extended.
Well, I took my whack at comparing the individual models against the observational data sets.
ReplyDeletehttp://rhinohide.wordpress.com/2010/08/11/mmh10-the-charts-i-wanted-to-see/
Deep, I found a few oddities. I raised some with Chad here.
ReplyDeleteUnfortunately I can't run their STATA code and am unfamiliar with the language.
Steven, it's a hard topic. But which tests did you have in mind?
ReplyDeleteHmmm, I may have been a bit hasty.
ReplyDeleteThe C.I. on LT is slightly wider than MT so that makes the adjusted second chart centre bin go up, not down. So 16 out of 57 models would be in the adjusted centre bin.
But the more I think about it, MMH's weighted model averaging is not really the same as a model run distribution anyway. It has the effect of bunching up the centre and distorting the spread that one would see using the distribution of 57 runs *or* the an unweighted distribution of model averages. In fact the MMH method in effect puts 23 of 57 runs (40%) in the central C.I. trend bin, whereas only 6 of 23 models or about 16 of 57 runs would be found there under normal weighting schemes.
What else ...
The trends are AC-corrected, so may have slightly different slopes, depending on the method used. So that could explain discrepancies with table 1.
But there's no question that the chart and table give different values for "models" LT and MT trends.
Anyway, I'm calculating simple linear trends (no AC correction) and getting similar results, so I'm not going to worry too much about these small discrepancies.
Deep,
ReplyDeleteI think their CI's are based just on trend uncertainty. So lots of runs will lie outside them. They've analysed as if the run sample is its own population - not from a larger pop, so the sort of mean se we're thinking of doesn't apply.
That's OK to a point, but you can only make conclusions about that set of runs, not models in general.
The trends are AC corrected in Table 1, so it still isn't clear why the se's (not the trends themselves) change in Table 2. But it ciuld be that they are somehow recalculated from the panel regression. We need a STATA expert.
With simple linear trends, my se's were about 1/4 those in Table 1.
On table 1 and table 2 comparison (rearranged for easy comparison).
ReplyDeleteTable x: DATASET LT trend (se) MT trend (se)
Table 1: UAH 0.070 (0.058) 0.040 (0.062)
Table 2: UAH 0.079 (0.060) 0.041 (0.056)
Table 1: RSS 0.157 (0.058) 0.117 (0.065)
Table 2: RSS 0.159 (0.058) 0.117 (0.057)
Very little matches in fact.
Of course, the error bars are for the mean, not the distribution. But the bars seem very tight. A simple se of the mean of the trends would be about 0.022.
ReplyDeleteCan you expand on that?
For the 23 MMH LT model trends in table 1 (sorry I haven't looked at MT), I get a mean of 0.243 and stdev of 0.073. Dividing by sqrt(23) yields an se for the mean estimate of 0.015.
But if I use a weighted distribution (as described above and in the paper), I get a mean of 0.262 (which matches the figures), and a stdev of 0.065.
Mean estimate s.e. then becomes 0.065 / (sqrt(N=23)) = 0.013. Which is exactly what is shown.
So it looks like the weighting scheme made a tight CI even tighter.
"Mean trend estimate s.e. then becomes 0.065 / (sqrt(N=23)) = 0.013. Which is exactly what is shown in MMH 2010."
ReplyDeleteI suppose the independence assumption would actually imply 0.065/ sqrt(N-1 = 22) = 0.014, which is higher (by 0.01) than the published s.e. figure. Perhaps this is an artifact of the panel regression. Or perhaps the independence assumption is used to combine the individual model s.e.'s in a way that results in the very low "models" trend s.e.
But, actually, if you look very closely at Figure 2, the models trend is 0.26 +/- 0.030 (se = 0.015), as opposed to 0.027C +/- 0.26 (se = 0.013) given in table 2.
Deep,
ReplyDeleteHave you seen Steve McI's latest post on mixed effects - between and within groups variance. He's saying that the se should be based on within groups variance - ie just trend variance, not model scatter. That corresponds to the way I thought they were doing it.
His exposition is not clear at all and is a red herring, IMHO.
ReplyDeleteThere is no clear explanation of where this exceedingly tight CI comes from. It just pops out "from the model". It is supposed to take autocorrelation in the constituent series into account, but other assumptions are less clear.
But maybe you could go through your calculation of 0.022 simple s.e. for "mean of the trends"?
I'm not sure how you got that ...
Deep,
ReplyDeleteYou're right, I made a mistake somewhere. Unfortunately I was using R interactively, so I don't have a script to check. I'll post a correction.
However, I think it's still true that the se used by MMH was based on model trend se, not the sd of spread of trends. That's what McI says should be used, and it seems to match.
Deep, Nick,
ReplyDeletedon't forget that the models also intercorrelate, and you have to use the full variance-covariance matrix when computing the s.e. for the ensemble mean. But of course the covariances aren't in the paper :-(
Martin,
ReplyDeleteThey aren't in the data supplied, that I can see, although they could be in some of the binary STATA intermediate files. They do model the covariance matrix in their Eq (11), though not lagged covariance.
"That's OK to a point, but you can only make conclusions about that set of runs, not models in general"
ReplyDeleteSeriously Nick. Is it indeed possible to ever falsify "models in general". You can only falsify what is presented as evidence, no?
Jonas B1
Anon "models in general"
ReplyDeleteWell, a statement about a particular subset of models is of limited interest. And people never make that qualification anyway. The message people take from a paper like this is "the models" aren't doing well.
But yes, you can make, and disprove proper statements about a general class, based on a sample. It's done all the time. Who do US voters favor in the next election? OK, ask 1000 of them. Does that represent the voters in general? Yes, if you're careful, and quote sampling error.
And it's the equivalent of sampling error that is at issue here. It's more complex than voting, because there are other sources of error too.