Tuesday, July 27, 2010

If it's hot in Washington, how about Montreal?

In one of Steve Goddard's posts at WUWT, there was some mocking of interpolation in GISS. "Is the temperature data in Montreal valid for applying to Washington DC.? " was asked.

Well, it turns out, yes it is, using anomalies. I looked in the raw GHCN data at McGill Montreal (71627/003), which has the only long GHCN record there, vs Washington NA (WMO 72405/000),  which also has a very long record. I used a 4-year tapered smoothing filter (triangle) on the monthly data. Here's how it turned out:




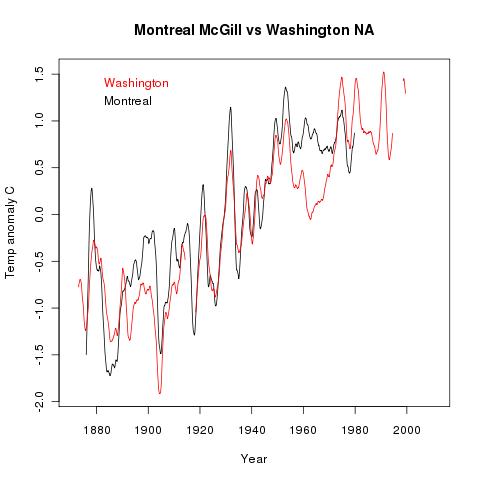
Anomalies are relative to each station mean over the period. Notice the slip at about 1915, where Montreal seems to go up about half a degree relative to Washington. It could well be a station move or change. This is just the sort of thing GISS type algorithms can pick up, even so far apart. But this is unadjusted data.
Posted by Nick Stokes at 6:21 PM

11 comments:

  1. Ron BrobergJuly 27, 2010 at 11:41 PM

    That's a nice visual.

    Is r^2 the best way to measure the actual correlation? Following up on Paolo's comment WUWT, is there to run through the entire set of stations -v- stations and map out either lat/lon regions with good correlation or at least get a rough definition of how correlation drops off with distance. Is there a latitudinal bias in correlation?

    ReplyDelete
  2. carrot eaterJuly 28, 2010 at 1:43 AM

    Ron

    Read Hansen 1987. It's all in there, though it bears being updated. Graphs of R vs distance, for different station pairs. This is the origin of the linear distance weight to 1200 km. There is absolutely a latitudinal bias. Correlation length is much further at high latitudes.


    Nick, I think you said one thing in that thread that rubbed me the wrong way. GISS always interpolates, no matter what, unless I'm quite mistaken. The basic concept is always to interpolate to the centerpoint of a subbox. It's just that the stations 1200 km away get very little weighting compared to the ones 100 km away, so if there are nearby stations, the far out ones don't have much of any influence.

    ReplyDelete
  3. Nick StokesJuly 28, 2010 at 7:35 AM

    CE, my point was that if you are operating on data and then taking a weighted sum (trend, average, whatever) then interpolating as an intermediate step has no special effect - it just ends up as a slightly different weighted sum.

    Let me put that algebraically. You have a data set x and calculate an average, global trend or whatever as w.x - a scalar product with weights w.

    Suppose you first make a new data set with interpolation. That's Z.x, where Z is some non-square matrix (creating new points). Then you calculate a modified sum W.(Z.x) with different weights W.

    That's just (W.Z).x. You've just created a different weighting w'=W.Z. You can express it with interpolation if you like, but it makes no essential difference.

    ReplyDelete
  4. EliRabettJuly 28, 2010 at 12:05 PM

    There is also a seasonal bias. See, for example New, Hulme and Jones. The correlation decay distance is about half in summer what it is in winter.

    ReplyDelete
  5. joeJuly 28, 2010 at 4:16 PM

    Nick;

    Thanks for showing this. I called Steve on this comment as well, and you've provided an excellent visual.

    Thanks to CE for that Hansen and Lebedeff reference. I hadn't seen that yet, and its an amazing paper. I'm not sure an update would help much, as it covers an impressive amount of material. Might be good to revisit and dust up the figures though for the snazzy iPad world.

    Great site Nick, interesting things going on here!

    ReplyDelete
  6. Nick StokesJuly 28, 2010 at 10:45 PM

    Joe, thanks for those kind words. It was actually your confidence on the anpmaly correlation that convinced me that I should test it. I think you would win your wager.

    ReplyDelete
  7. EliRabettJuly 28, 2010 at 11:28 PM

    Nick, that is true except where there is no data, which is why using the longer/shorter correlation distances as a function of season and latitude might be useful in the polar regions

    ReplyDelete
  8. Nick StokesJuly 29, 2010 at 8:23 AM

    Eli, I did compute the anomaly using the monthly averages. I then smoothed the monthly plot, which of course wiped out any seasonal effect. I could do the seasons separately, but the point of this exercise was just to show that a commonly asserted belief in absence of correlation was wrong in an instance cited.

    ReplyDelete
  9. stevenJuly 31, 2010 at 2:59 AM

    Nice nick.

    There is also the paper I linked to over at WUWT. its basically an update of hansen 87. fills in some of the blanks WRT seasonality and more detail on latitude.

    I like Rons idea,

    ReplyDelete
  10. carrot eaterJuly 31, 2010 at 3:49 AM

    what paper is that? i'm not going to go searching through WUWT for the citation

    ReplyDelete
  11. stevenJuly 31, 2010 at 11:55 AM

    Lets see.

    http://hadobs.metoffice.com/hadghcnd/HadGHCND_paper.pdf

    I read it a while back as did kennth fritsch. nobody wants to discuss it.

    Anyways, they did some interesting things with looking not just at radius by at angle( I recall0 the insight being that if you have a flow the correlation is going to vary as a function of the direction of the flow.. conceptually speaking

    ReplyDelete

Subscribe to: Post Comments (Atom)