This is a follow-up to this earlier post, which please see for details. I had got into some difficulty there with using the R function nlm() to estimate both the regression parameters and the delay coefficients for each of the exogenous variables Vol, Sol and ENSO. The solar variable, which interacts most weakly, was apt to be assigned zero or negative delay, which created constant or exponentially rising secular processes, which were used by the fit.
I could avoid this by constraining that parameter. But I think it is better to do as others have done and use a common delay for all three. There is reasonable physical justification for that, and it reduces overfitting.
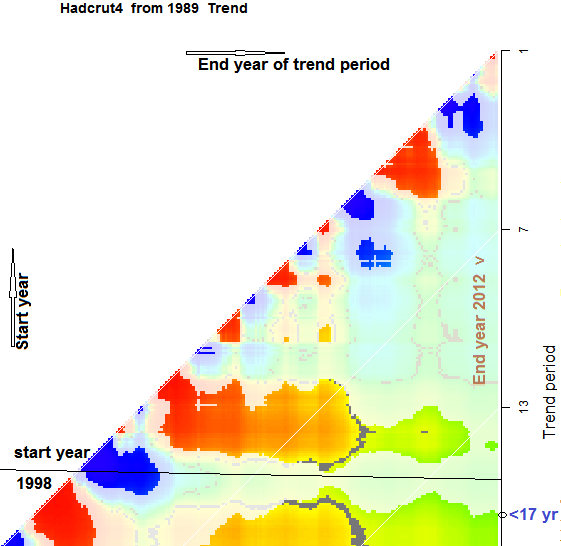
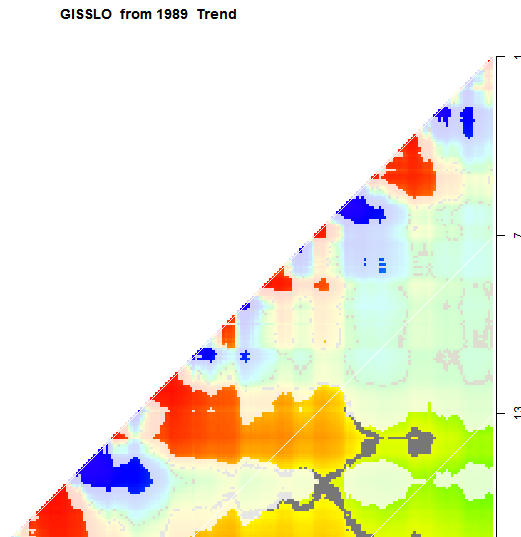
The result is a much more stable trend pattern across the time intervals and data sets. The trends since 1997 are now mostly between 0.65 °C/century and 1.325. This might still be seen as a slowdown, but surely a minor one. Oddly the only exception is the case studied by SteveF, Hadcrut 4 with linear from 1950. The trend I got there was 0.117°C/cen, I think quite similar to his, as was the decay coefficient at 0.026 (cf his 0.031).
I'll show below the revised table and images.
A zip file of R code and data is here.
Results
Here is the table. The results look better in several ways:
- The coefficients are reasonably comparable across cases
- Adding a quadratic term now always reduces the sum of squares
- The post-1997 trends are fairly uniform
| Start | Trend | 1 | Vol | Sol | ENSO | t | t^2 | Delay | SS | |
| HADCRUT4 | 1950 | 0.117 | 2e-04 | -8.39135 | -3e-05 | 0.42995 | 0.25141 | NA | 0.02584 | 10.079 |
| HADCRUT4 | 1950 | 1.024 | -0.07304 | -2.27873 | 0.00048 | 0.14844 | 0.30742 | 0.21653 | 0.12729 | 8.254 |
| HADCRUT4 | 1979 | 1.086 | -0.01689 | -2.72106 | 0.00069 | 0.13331 | 0.50485 | NA | 0.11706 | 3.909 |
| HADCRUT4 | 1979 | 1.078 | -0.00963 | -2.82278 | 0.00069 | 0.13478 | 0.50155 | -0.07812 | 0.11325 | 3.893 |
| GISS | 1950 | 0.787 | -0.00116 | -6.00112 | 5e-05 | 0.24419 | 0.34476 | NA | 0.04173 | 10.441 |
| GISS | 1950 | 1.246 | -0.04836 | -2.70426 | 0.00042 | 0.1288 | 0.37122 | 0.14273 | 0.11017 | 9.626 |
| GISS | 1979 | 1.325 | -0.01623 | -3.28644 | 0.00065 | 0.1334 | 0.49335 | NA | 0.09649 | 5.086 |
| GISS | 1979 | 1.315 | -0.01142 | -3.38601 | 0.00064 | 0.13513 | 0.48994 | -0.05241 | 0.09342 | 5.079 |
| NOAA | 1950 | 0.65 | -0.00121 | -4.42051 | 0.00017 | 0.19036 | 0.33218 | NA | 0.06223 | 8.103 |
| NOAA | 1950 | 0.877 | -0.04486 | -2.39086 | 0.00042 | 0.13126 | 0.34807 | 0.13221 | 0.118 | 7.351 |
| NOAA | 1979 | 0.929 | -0.01586 | -2.81475 | 0.00059 | 0.12721 | 0.47137 | NA | 0.10492 | 3.581 |
| NOAA | 1979 | 0.913 | -0.00629 | -2.99252 | 0.00058 | 0.13034 | 0.46551 | -0.10409 | 0.09849 | 3.554 |
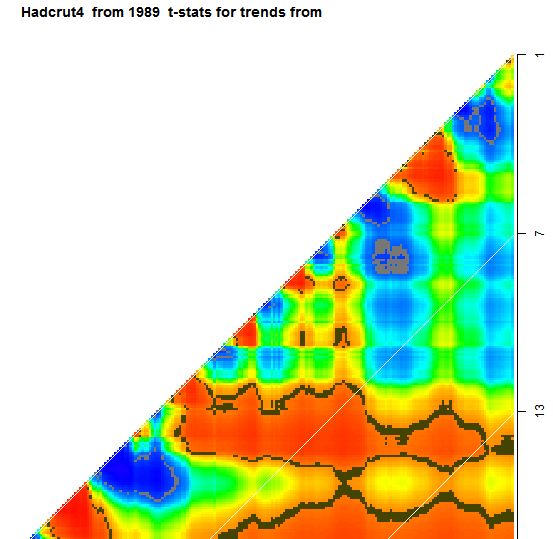
Images
The images may be scanned in the viewer below. There are 24, and you can flip through them using the top buttons. But you can also subselect using the selection boxes. For example, if you choose GISS, you will then cycle through just the 8 GISS plots. If you ask as well for plot type components, you will cycle through the four component plots. etc.
Data Start Year Regressor Plot type |
SteveF has had difficulty getting comments through the system - I'm trying to find out why. Anyway, he sent by email these comments, and I'll just follow with a few points I made in reply - hope we can get comments working for him soon: SteveF says: I think I may have identified why the influence of the solar cycle increases in the 1979 to present analyses compared to the 1950 to present analyses: there is a coincidental congruence between the 1983 and 1991 volcanoes and the peak (or near peak) of the solar cycle. That is, the downward part of the solar cycle is aliased with the volcanic influence. In the longer series, this influence is diluted in the regression, though for certain is still influencing the results. The 1964 to 1970 eruptions, while weaker, do not coincide with the peak of the solar cycle. I have tried several things to straighten this out, so far without a lot of success. I will next try a regression from 1950 to 1975 to see if the solar cycle influence falls to almost nothing (or even negative!) as I suspect it will. Substituting a regression specified quadratic or cubic secular function. I think a defensible argument is, absent a good physical rational, that the best approach is to simply sum the two radiative terms (both with watts/M^2 units) and see what happens to the diagnosed "optimal lag". Any regression that reports a physically implausible lag constant for best fit seems to me very suspect. There have been multiple published reports with estimated lags for volcanoes; a tau value near 30-36 months for the decay of the response seems to be a common, though the exact value depends weakly on assumed climate sensitivity value (I have independently verified this is correct). Perhaps the best thing is to just try a few lags in the credible range and see what the best fit regression constants turn out to be. I also note that very much higher solar than volcanic response (on a watt/M^2 basis) is exactly the opposite of what I would expect on physical grounds; the slower solar cycle response ought to be lower, on a degrees/watt/M^2 basis than the volcanic, because the 11 year solar cycle 'sees' slower responding (deeper) parts of the oceans more than the shorter volcanic forcing. If one accepts a large discrepancy between the measured changes in solar intensity over the cycle and the size of the temperature response, then some kind of 'amplification' of the solar cycle must be responsible (eg. more low clouds at the minimum), and evidence for that seems lacking. Of course, even if one assumes the true solar cycle forcing (in watts/M^2) is far higher than the measured changes in solar intensity, that doesn't mean there should not be considerable lag in the temperature response. Finally, I tried a linear secular trend starting in 1964 (to include the earlier volcanoes); the fit is improved compared to starting in 1950 and the discrepancies between model and Hadley global temperatures is much reduced. Perhaps you could try that as well. Nick says: I can well imagine that solar cycles might get tangled with volcanoes. My experience was the the solar cycle, being weak, could be pushed around a lot by the optimisation process - both the linear and the lag fitting. It had a strong tendency to drift into zero or negative lag, which nlm() took advantage of to create spurious fitting functions. For the same reasons, I don't take too much notice of the amplitude that emerges from regression. It could be just taking up a bit of the volcano signal. My main concern at the moment is with the use of Nina34. I think it's a sensitive index, but also includes warming trend, and when you adjust with it, it takes out that part. I'm inclined now to switch to SOI, which may not be as good, but can't drift. A practical alternative is to detrend Nina34, but harder to justify, and the detrend would depend on the interval. I'd be happy to try a 1964 start. Another option is to use GHG forcing as one of the regressor functions.