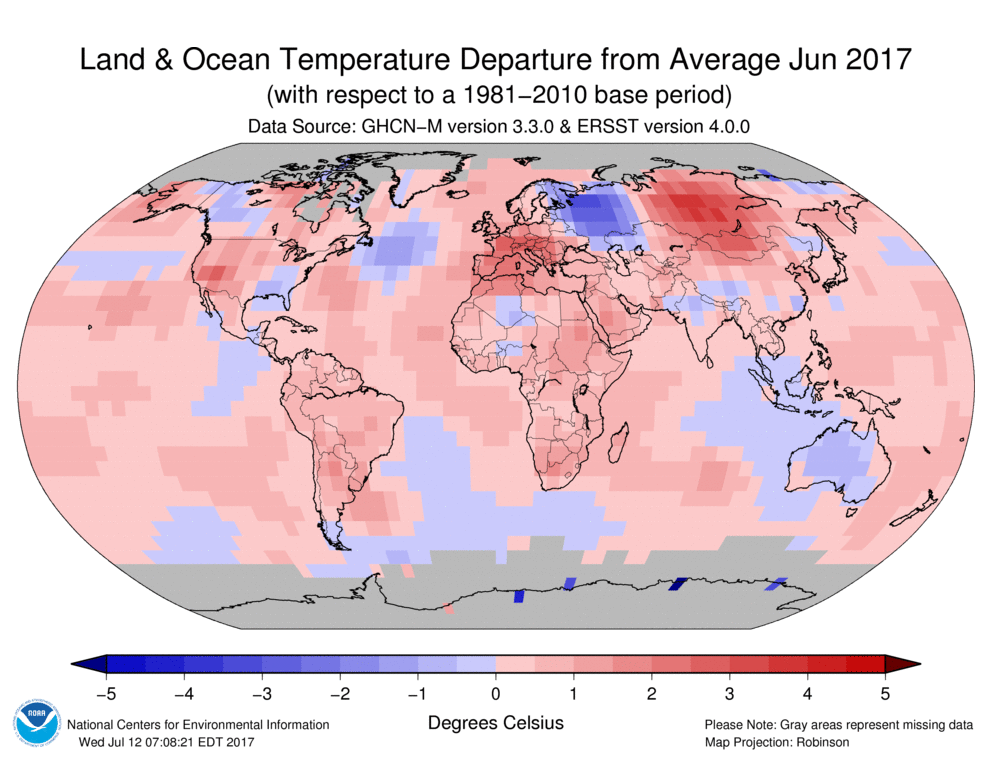
This post is about some exaggerated accounts that circulate about past forest fires. The exaggeration had been part of a normal human tendency - no-one cares very much whether accounts of events that caused suffering inthe past may be inflated, and so the more dramatic stories win out. But then maybe it does begin to matter.
I have two topics - the history of wildfire in the US, and a particular fire in Victoria in 1851. When people start to wonder about whether fires are getting worse in the US, as they seem to be, then a graph is trotted out to show how much worse things were in the 1930's. And if there is a bad fire in Australia, the 1851 fire is said to be so much worse. This is all to head off any suggestion that AGW might be a contributor.
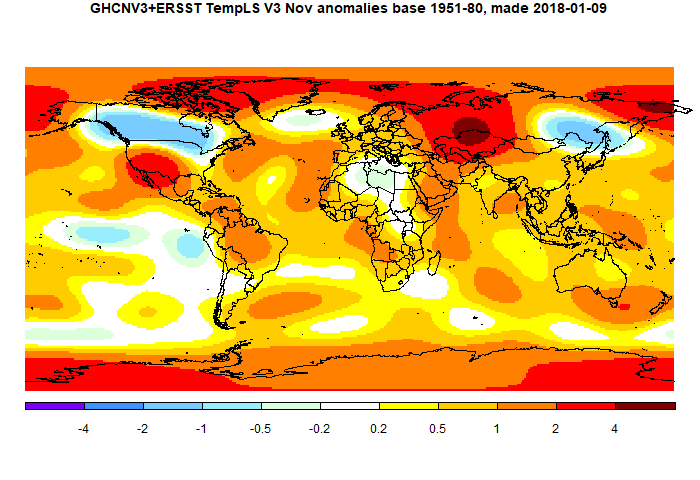
I'll start with the US story. The graph that appears is one like this:
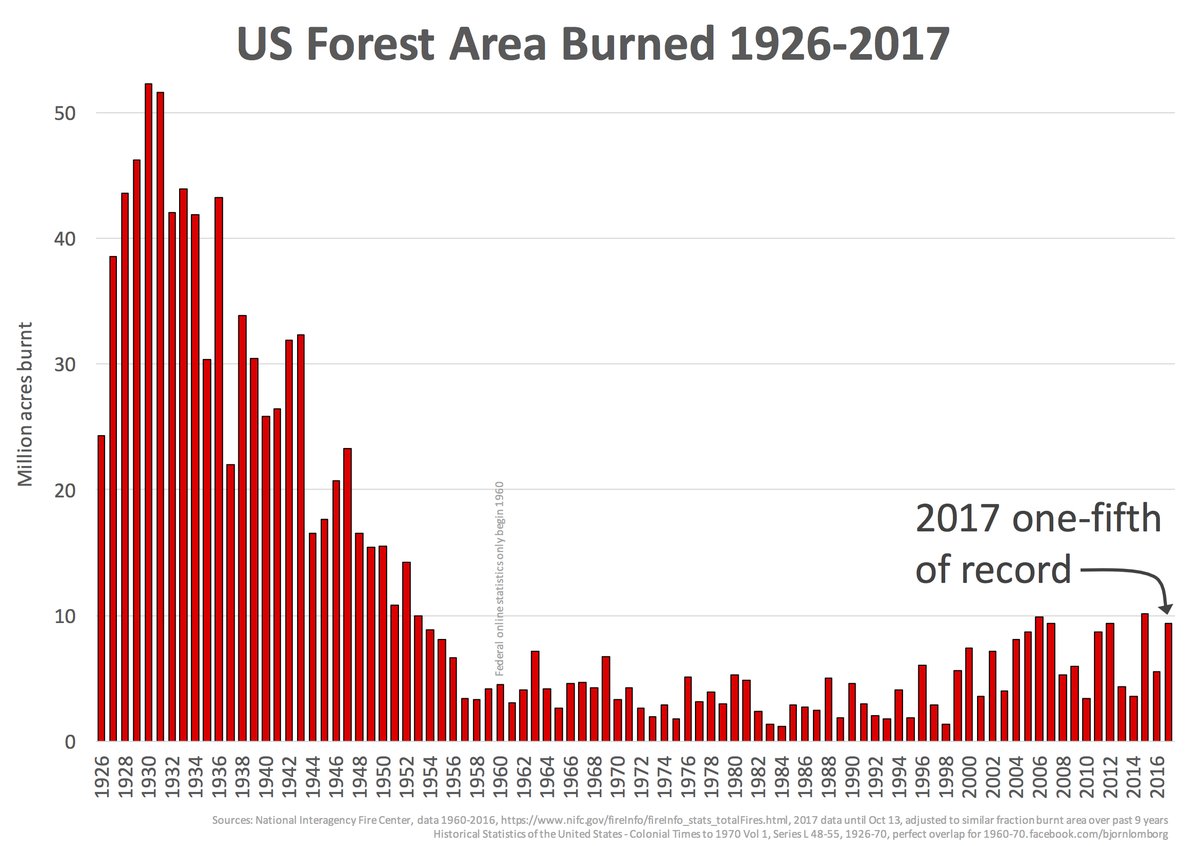
This appeared in a
post by Larry Kummer a few days ago. He gave some supporting information, which has helped me to write this post. I had seen the plot before, and found it incredible. The peak levels of annual burning, around 1931, are over 50 million acres, or 200,000 sq km. That is about the area of Nebraska, or 2.5% of the area of ConUS. Each year. It seems to be 8% of the total forest area of ConUS. I'm referring to ConUS because
it was established that these very large figures for the 1930's did not include Alaska or Hawaii. It seemed to me that any kind of wildfires that burnt an area comparable to Nebraska would be a major disaster, with massive loss of life.
So maybe the old data include something other than wildfires. Or maybe they are exaggerated. I wanted to know. Because it is pushed so much, and looks so dodgy, I think the graph should not be accepted.
Eli has just put up a
post on a related matter, and I commented there. He helpfully linked to previous blg discussions at
RR and
ATTP
Larry K, at JC's, traced the origin of the graph to a
2014 Senate appearance by a Forestry Professor (Emeritus), David South. He is not a fan of global warming notions. Rather bizarrely, he took the opportunity of appearing before the Senate committee to offer a bet on sea level:
"I am willing to bet $1,000 that the mean value (e.g. the 3.10 number for year 2012 in Figure 16) will not be greater than 7.0 mm/yr for the year 2024. I wonder, is anyone really convinced the sea will rise by four feet, and if so, will they take me up on my offer?"
Prof South's graph did not come from his (or anyone's) published paper; he has not published on fire matters. But it was based on real data, of a sort. That is found in a document on the census site:
Historical Statistics of the United States p537. That is a huge compendium of data about all sorts of matters. Here is an extract from the table:

As you can see, the big numbers from the 30's are in "unprotected areas". And of these, the source says:
"The source publication also presents information by regions and States on areas needing protection, areas protected and unprotected, and areas burned on both protected and unprotected forest land by type of ownership, and size of fires on protected areas. No field organizations are available to report fires on unprotected areas and the statistics for these areas are generally the best estimates available."
IOW, an unattributed guess. That that is for the dominant component. Federal land fires then are basically less than modern.
The plot mostly in circulation now, and shown by Larry K above, is due to
a Lomborg facebook post.
The organisation currently responsible for presenting US fire history statistics is the National Interagency Fire Center. And their
equivalent table lists data back to 1960, which pretty much agrees where it overlaps with the old census data to 1970. But they rather pointedly go back no further. And at the bottom of the table, they say (my bold):
"Prior to 1983, sources of these figures are not known, or cannot be confirmed, and were not derived from the current situation reporting process. As a result the figures above prior to 1983 shouldn't be compared to later data."
So not only do they not show data before 1960; they advise against comparison with data before 1983.
Interestingly, ATTP noted that a somewhat similar graph appeared on a USDA Forest Service at
this link. It now seems to have disappeared.
I think these graphs should be rejected as totally unreliable.
The Victorian Bushfires of 1851.
First some background. Victoria was first settled in 1834, mainly around Melbourne/Geelong (Port Phillip District), with a smaller area around Portland in the West. In Feb 1851, the time of the fires, the region was still part of the colony of New South Wales. Two big events to come later in the year were acquiring separate colony status, and the discovery of gold, which created a gold rush. But in Feb, the future colony had about 77,000 people, mainly around Melbourne/Geelong. There were no railways or telegraphs, and no real roads outside that region.
There undoubtedly was a very hot day on Thursday Feb 6, 1851, and the populated area was beset with many fires. It may well have been the first such day in the seventeen years of the region, and it made a deep impression.
This site gathers some reports. But the main furphy concerns claims of statewide devastation.
Wiki has swallowed it:
"They are considered the largest Australian bushfires in a populous region in recorded history, with approximately five million hectares (twelve million acres), or a quarter of Victoria, being burnt."
A quarter of Victoria! But how would anyone know? Nothing like a quarter of Victoria had been settled. Again, virtually no roads. No communications. Certainly no satellites or aerial surveys. Where does this stuff come from?
It is certainly widespread. The ABS, (our census org) says
"
The 'Black Thursday' fires of 6 February 1851 in Victoria, burnt the largest area (approximately 5 million ha) in European-recorded history and killed more than one million sheep and thousands of cattle as well as taking the lives of 12 people (CFA 2003a; DSE 2003b)"
It is echoed on the site of the
Forest Fire Management (state gov) .The 1 million sheep (who counted them?) and 12 people are echod in most reports. But the ratio is odd. People had very limited means of escape from fire then, and there were no fire-fighting organisations. No cars, no roads, small wooden dwellings, often in the bush. Only 12, for a fire that burnt a quarter of Victoria?
The ABS cites the CFA, our firefighting organisation. I don't know what they said in 2003, but what they
currently list is the 12 people killed, and 1000000 livestock, but not the area burnt.
By way of background, here is a survey map of Victoria in 1849. The rectangles are the survey regions (counties and parishes). It is only within these areas that the Crown would issue title to land. That doesn't mean that the areas were yet extensively settled; the dark grey areas are currently purchased. I think even that may be areas in which there are purchases, rather than the area actually sold.

There are a few small locations beyond - around Horsham in the Wimmera, Port Albert, in Gippsland, Portland, Kyneton and Kilmore. This is a tiny fraction of the state. So even if a quarter of the state had burnt, who would be in a position to assess it?
So what are the original sources? Almost entirely a few newspaper articles.
Here is one from the Melbourne Argus, on Monday 10th Feb, four days after the fire. They explain why they judiciously waited:
"In our Saturday's issue we briefly alluded to the extensive and destructive bush fires that prevailed throughout the country, more particularly on the Thursday preceding. Rumours had reached us of conflagrations on every side, but as we did not wish to appear alarmists, we refrained from noticing any but those that were well authenticated, knowing how exceedingly prone report is to magnify and distort particulars. Since then, however, we learn with regret that little only of the ill news had reached us, and that what we thought magnified, is unhappily very far from the fearful extent of the truth."
And they give an exceedingly detailed listing of damages and losses, but all pretty much within that surveyed area. A large part of the report quotes from the Geelong Advertiser. There is a report from Portland, but of a fire some days earlier. Many of the fires described are attributed to some local originating incident.
There is an interesting 1924 account
here by someone who was there, at the age of 12 (so now about 85). It gives an idea of how exaggerated notions of area might have arisen. He says that the conflagration extended from Gippsland northward as far as the Goulburn river. But even now, a lot of that country is not much inhabited. It's pretty clear that he means that fires were observed in Gippsland (a few settlements) and the Goulburn (probably Seymour).
So again, where does this notion of 5 million hectares come from? I haven't been able to track down an original source for that number, but I think I know. Here (from
here) is a common summary of the regions affected
"'Fires covered a quarter of what is now Victoria (approximately 5 million hectares). Areas affected include Portland, Plenty Ranges, Westernport, the Wimmera and Dandenong districts. Approximately 12 lives, one million sheep and thousands of cattle were lost'"
Those are all localities, except for the Wimmera, which is a very large area. But the only report from Wimmera is of a fire at Horsham, virtually the only settled area. Another formulation is from the CFA:
"Wimmera, Portland, Gippsland, Plenty Ranges, Westernport, Dandenong districts, Heidelberg."
Apart from the western town Portland, and "Wimmera", the other regions are now within the Melbourne suburbs (so they left out Geelong and the Barrabool ranges, which seems to have been seriously burnt). So where could 5 million hectares come from? I think from the reference to Wimmera. Some reports also list Dandenong as Gippsland, which is a large area too. I think someone put together the Wimmera, which has no clear definition, but Wiki
puts it at 4.193 million hectares. With a generous interpretation of Westernport and Portland, that might then stretch to 5 million hectares. But again, Wimmera has only one settled location, Horsham, where there was indeed a report of a fire.