The GISS V4 land/ocean temperature anomaly was 1.26°C in September, down from 1.3°C in August. This drop was similar to the 0.071°C fall reported here for TempLS.
As with TempLS, September broke a sequence of fifteen record months- September 2023 was 1.48°C, but next was 2020 at 0.96°C.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
Tuesday, October 22, 2024
Saturday, October 19, 2024
September global surface TempLS down 0.071°C from August.
The TempLS FEM anomaly (1961-90 base) was 1.094°C in September, down from 1.165°C in August. It was a record in a way - it is the first month of the last 16 that was not a record warm. September 2023 was 1.21°C; however last month was warmer than any September before 2023.
This month's posting has been delayed by the late posting of results from NOAA, which was affected by the floods in Asheville.
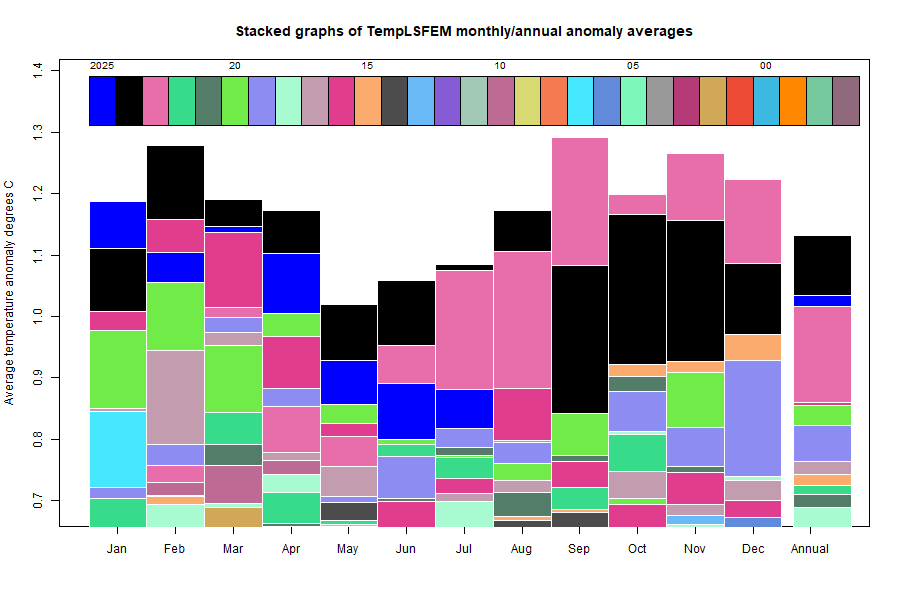
Here is the corresponding stacked graph, showing how much hotter recent months have been:
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
This month's posting has been delayed by the late posting of results from NOAA, which was affected by the floods in Asheville.
Here is the corresponding stacked graph, showing how much hotter recent months have been:

Here is the temperature map, using the FEM-based map of anomalies. Use the arrows to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Friday, October 11, 2024
When regression doesn't work - Florida hurricanes
Firstly an apology - no TempLS yet for September. The reason is floods in Asheville, where the NOAA GHCN data comes from (in better times).
I'm writing about a post by Roy Spencer on the statistics of major hurricanes landfalling in Florida. His data comes from this Wiki table. He does a plot of intensity of major hurricanes against time:
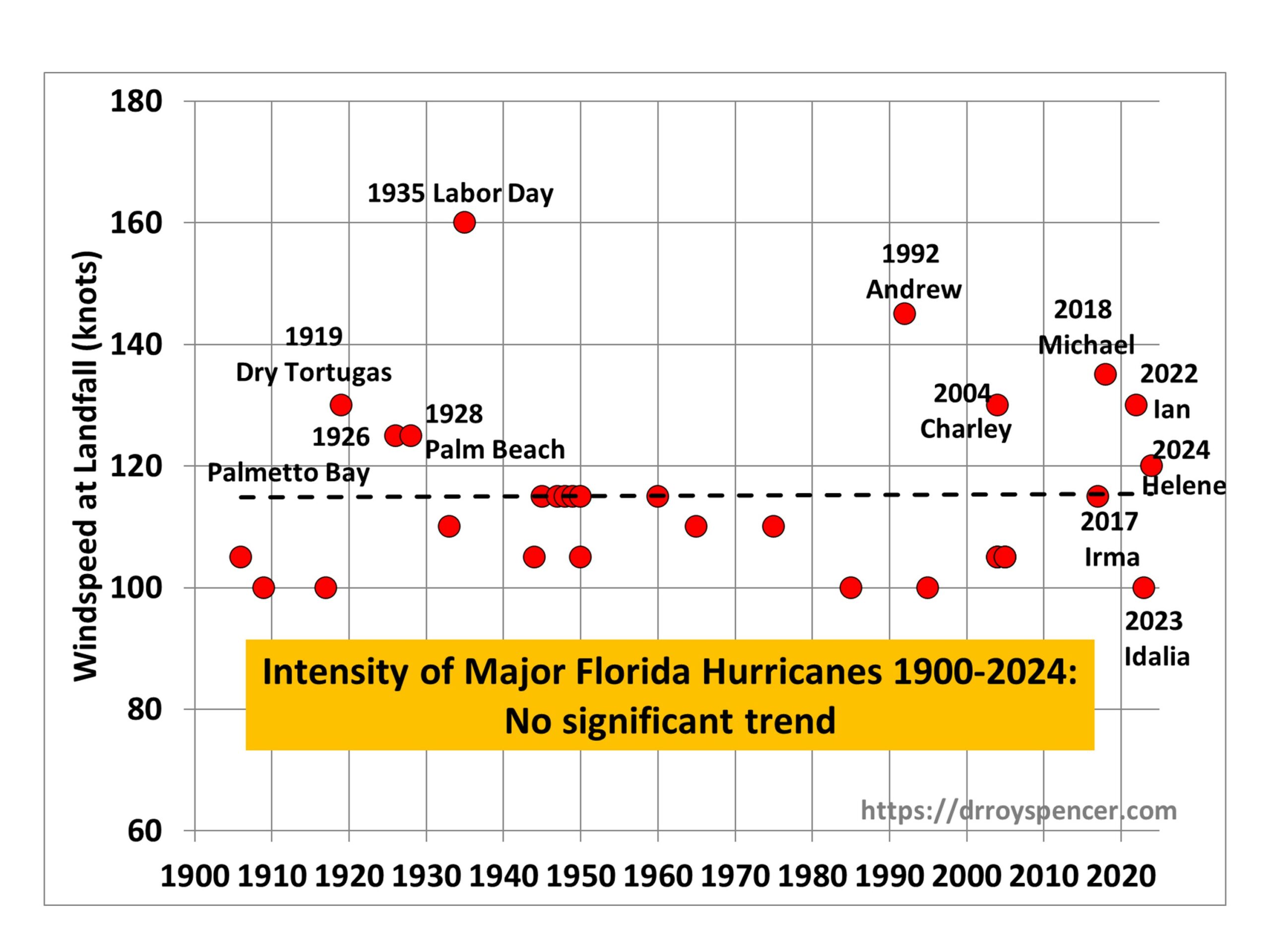
He goes through the regression arithmetic (without error) to yield the flat line shown. So no trend? This exciting result is already doing the rounds.
The problem is one of censored data. Regression allows you to have data y with irregular spacing in t, on the assumption that there is a linear model
y=a*t+b+ε
where a and b are parameters that you estimate by fitting, and ε is a set of random residuals with mean zero (you can also estimate the sd). Put another way, the assumption is that missing data is statistically similar to the data sampled.
But here the missing years are not like that. We don't know the numbers (they were below Wiki's cut-off) but we know they were less than 100. That is what censored data means. And that just doesn't fit with the regression model.
You can see this with a simple case. Suppose we had just the 1935 hurricane, at 160 mph, and the 1992 one at 145 mph. Regression would give a down trend. But then you include the 1933 hurricane at 110. That is another big hurricane back then, so it should lower the trend further, no? No! The regression effectively averages the two to 135 mph, so now there is an uptrend. The reason is that the first regression assumed the 1933 value would be about 160. When it finds out that it is much lower, the trend goes up. And if it found out that 1934 was even lower, the trend would go up even further. And of course we do know that 1934 was less than 100.
This might seem like an artefact of too few data. So let's see it played out on a larger scale. Suppose in every year from 1906 to 1955, when there wasn't a major hurricane, we add one with strength 100 mph. That has to mean that the past was windier, right? And the trend is more negative. But no, the trend goes from Roy's -0.002 mph/year to 0.127 mph/year. Here is the plot, with trend and points after the strengthening of early hurricanes in blue:
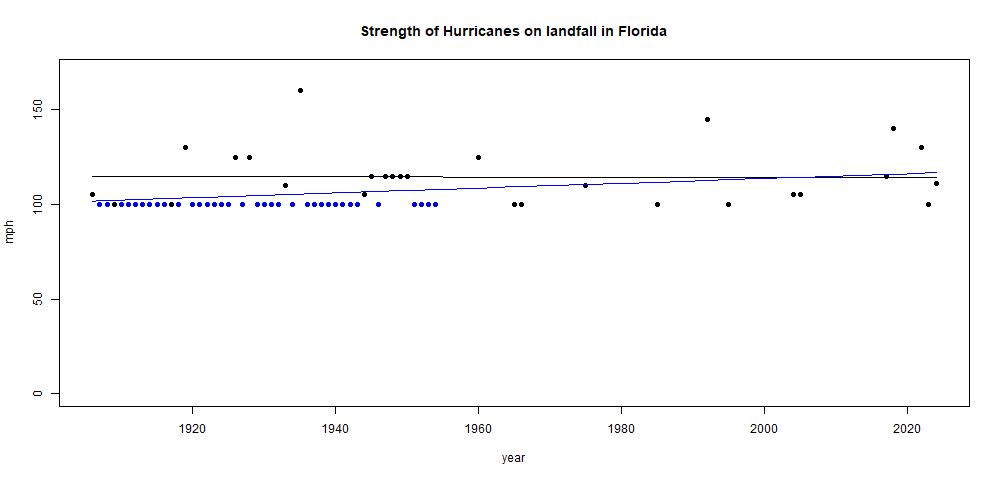
So what is the right thing to do? I'm not an expert in censored data, so I don't know. But I do know this won't work. You can see intuitively that in the last 34 years, there have been 5 hurricanes greater than 118. There were only 4 in the previous 90. That does indicate strengthening.
Roy did a second regression, on numbers of major hurricanes
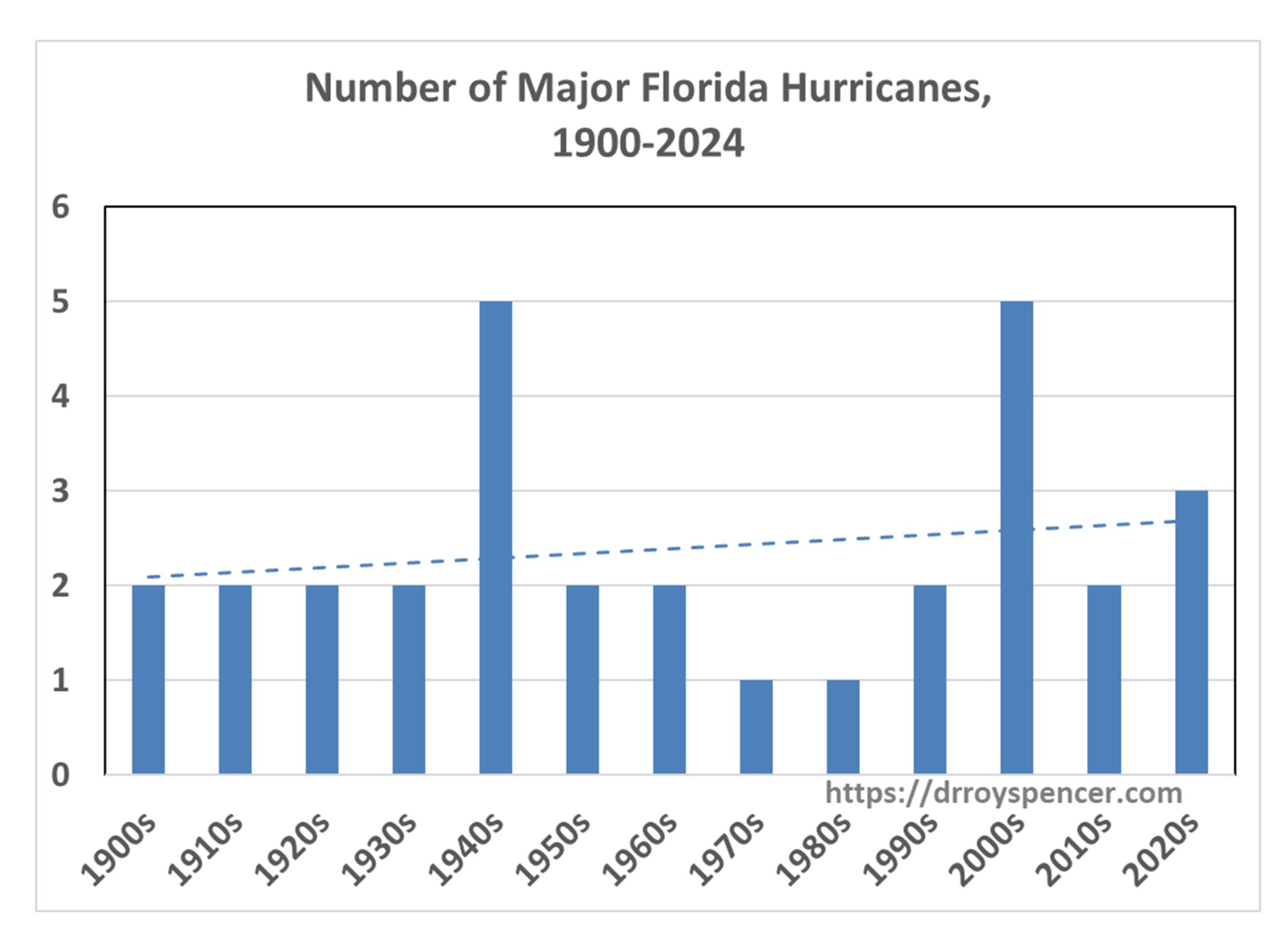
This doen't have the same objection, because of the binning into decades. There are no missing data (except in the last decade). Years that had no major hurricanes were correctly assigned value zero in the binning. And yes, the trend is up. So this plot is not the one that is circulating.
I'm writing about a post by Roy Spencer on the statistics of major hurricanes landfalling in Florida. His data comes from this Wiki table. He does a plot of intensity of major hurricanes against time:

He goes through the regression arithmetic (without error) to yield the flat line shown. So no trend? This exciting result is already doing the rounds.
The problem is one of censored data. Regression allows you to have data y with irregular spacing in t, on the assumption that there is a linear model
y=a*t+b+ε
where a and b are parameters that you estimate by fitting, and ε is a set of random residuals with mean zero (you can also estimate the sd). Put another way, the assumption is that missing data is statistically similar to the data sampled.
But here the missing years are not like that. We don't know the numbers (they were below Wiki's cut-off) but we know they were less than 100. That is what censored data means. And that just doesn't fit with the regression model.
You can see this with a simple case. Suppose we had just the 1935 hurricane, at 160 mph, and the 1992 one at 145 mph. Regression would give a down trend. But then you include the 1933 hurricane at 110. That is another big hurricane back then, so it should lower the trend further, no? No! The regression effectively averages the two to 135 mph, so now there is an uptrend. The reason is that the first regression assumed the 1933 value would be about 160. When it finds out that it is much lower, the trend goes up. And if it found out that 1934 was even lower, the trend would go up even further. And of course we do know that 1934 was less than 100.
This might seem like an artefact of too few data. So let's see it played out on a larger scale. Suppose in every year from 1906 to 1955, when there wasn't a major hurricane, we add one with strength 100 mph. That has to mean that the past was windier, right? And the trend is more negative. But no, the trend goes from Roy's -0.002 mph/year to 0.127 mph/year. Here is the plot, with trend and points after the strengthening of early hurricanes in blue:

So what is the right thing to do? I'm not an expert in censored data, so I don't know. But I do know this won't work. You can see intuitively that in the last 34 years, there have been 5 hurricanes greater than 118. There were only 4 in the previous 90. That does indicate strengthening.
Roy did a second regression, on numbers of major hurricanes

This doen't have the same objection, because of the binning into decades. There are no missing data (except in the last decade). Years that had no major hurricanes were correctly assigned value zero in the binning. And yes, the trend is up. So this plot is not the one that is circulating.