I am planning to add station data to the GHCN V3 monthly portal. Not monthly data which would be cumbersome, but annual average. This is useful for plotting and trends.
There is a trial below. Each link leads to the NOAA GHCN station summary, as before, but the radio button brings up a page with a table of the annual averages, along with a brief metadata and a map (the station is in the middle). There is a table for unadjusted data, and below for adjusted. Both are then repeated in CVS format, for import into Excel. The table of links is searchable (Ctrl-F), and can take a while to load. I'll probably add a graphing and trend calculation capability.
In calculating the annual averages, I eliminated years with less than 9 months data. I also (before) removed data with flags indicating unreliability. Then I infilled missing months with the overall mean for that station/month (else seasonal effects add a lot of noise). Then I calculated the simple average of the infilled data.
Thursday, March 26, 2015
Friday, March 20, 2015
Central Australian warming
I've been arguing again, at Climate Etc. Blogger Euan Mearns has a guest post in which he claims to demonstrate that stations within 1000km of Alice Springs show no warming.
I'll post about it here, because it illustrates the averaging fallacies I've been writing about regarding Steven Goddard and colleagues (also here). And also because "Alice Springs" is one of those words naysayers sometimes throw at you as if no further explanation is required (like Reykjavik). People who do that generally don't know what they are talking about, but I'm curious, since I've been there.
There are actually two issues - the familiar time series of averages of a varying set of stations, and anomalies not using a common time base. I'll discuss both.
The stations are obtained from the GISS site. If you bring up Alice Springs, it will indicate other stations within a radius of 1000 km. My list was 29, after removing repetitions. I've given here a list of the stations, together with the calculated trends (°C/century) and the long term normals. For all calculations I have used annual averages, discarding years with fewer than nine months data. The annual data (unadjusted GHCN V3 monthly from here) that I used is in CSV form here.
So Euan's post shows a time series of whetever reported in each year:

And, sure enough, not much trend. But he also showed (in comments) the number of stations reporting

Now what his average is really mainly showing is whether that highly variable set has, from year to year, hotter or colder locations. To show that, as usual I plot the same averaging process applied to just the station normals. This has no weather aspect:
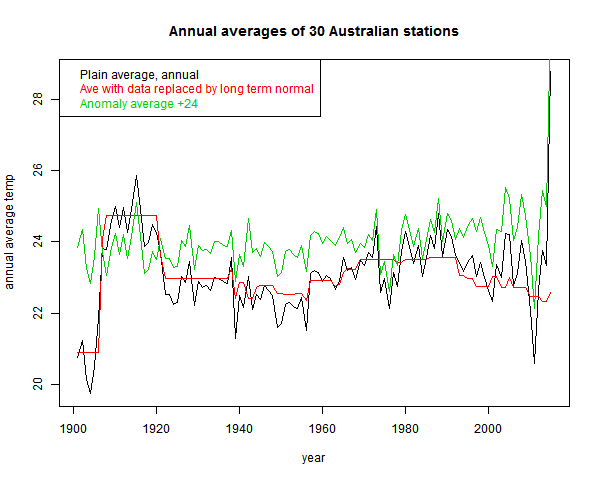
You see the red curve. That incorporates much of the signal that the fallacious black curve includes.
The effect is not as severe as Goddard's, because the stations are more homogeneous. The range of normal variation is less. It can be reduced, of course, by subtracting the mean. That is the green "anomaly" plot that I've shown. It is more regular, but still not much trend. That brings up the anomaly fallacy.
This is the fault of comparing anomalies using varying base intervals. I've described it in some detail here. If the stations have widely different periods of data, then the normals themselves incorporate some of the trend. And subtraction removes it.
This is a well-known problem, addressed by methods like "common anomaly method" (Jones), "reference stations method" (GISS), "first difference method" (NOAA). I mention these just to say that it is a real problem that major efforts have been made to overcome.
As a quick and mostly OK fix, I recommend using regression fits for a common year, as described here. But the more complete method is a combined regression as used in TempLS (details here)
Update - to be more specific, as in the link it is best to do this in conjunction with some scheme for preferring data local to a region. There I used weighting. But to stick closest to the convention of using a fixed interval like 1961-90, my process would be:
1. If there is enough data in that interval (say 80%) use the regression mean over the interval
2. If not, then extend the interval to the minimum extent necessary to get 30 (or 24) years of data.
So I've done a combined regression average:
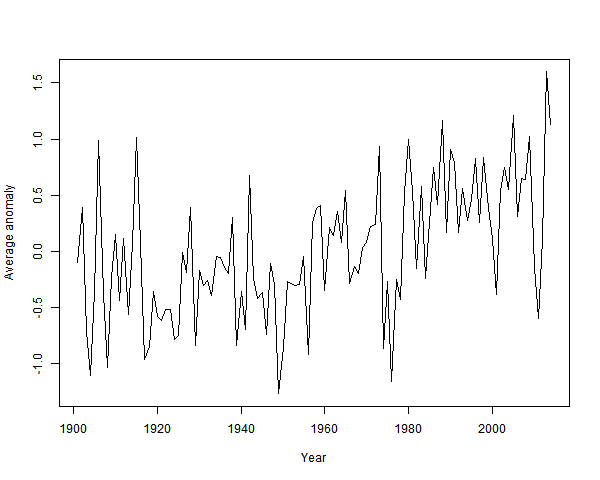
It's clearly warming since about 1940. And by about a degree.
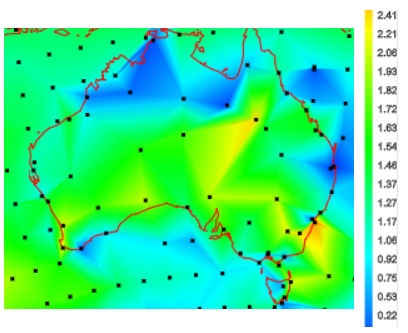
The station trends over their observed periods are almost all positive. So they are over a fixed period. Here, from the active trend map is a snap of trends in Australia since 1967:
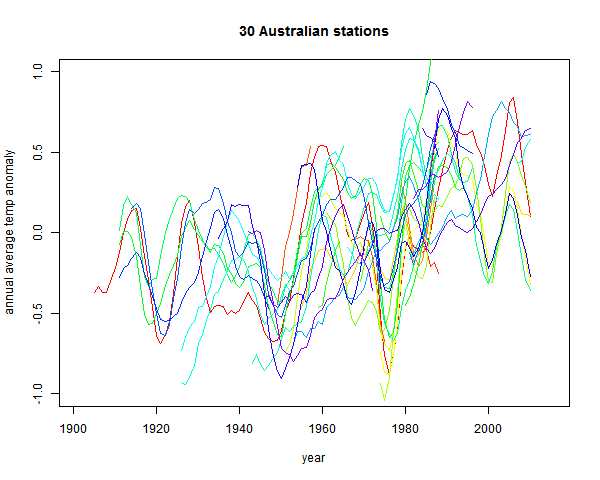
Plots of the station data are somewhat obscured by noise. From Climate Etc:

It is rising. But a modest degree of smoothing - a 9 point triangular filter, gives:
The uptrend is now unmistakeable.
I'll post about it here, because it illustrates the averaging fallacies I've been writing about regarding Steven Goddard and colleagues (also here). And also because "Alice Springs" is one of those words naysayers sometimes throw at you as if no further explanation is required (like Reykjavik). People who do that generally don't know what they are talking about, but I'm curious, since I've been there.
There are actually two issues - the familiar time series of averages of a varying set of stations, and anomalies not using a common time base. I'll discuss both.
The stations are obtained from the GISS site. If you bring up Alice Springs, it will indicate other stations within a radius of 1000 km. My list was 29, after removing repetitions. I've given here a list of the stations, together with the calculated trends (°C/century) and the long term normals. For all calculations I have used annual averages, discarding years with fewer than nine months data. The annual data (unadjusted GHCN V3 monthly from here) that I used is in CSV form here.
The Goddard Fallacy
So Euan's post shows a time series of whetever reported in each year:
And, sure enough, not much trend. But he also showed (in comments) the number of stations reporting
Now what his average is really mainly showing is whether that highly variable set has, from year to year, hotter or colder locations. To show that, as usual I plot the same averaging process applied to just the station normals. This has no weather aspect:

You see the red curve. That incorporates much of the signal that the fallacious black curve includes.
The effect is not as severe as Goddard's, because the stations are more homogeneous. The range of normal variation is less. It can be reduced, of course, by subtracting the mean. That is the green "anomaly" plot that I've shown. It is more regular, but still not much trend. That brings up the anomaly fallacy.
The anomaly fallacy
This is the fault of comparing anomalies using varying base intervals. I've described it in some detail here. If the stations have widely different periods of data, then the normals themselves incorporate some of the trend. And subtraction removes it.
This is a well-known problem, addressed by methods like "common anomaly method" (Jones), "reference stations method" (GISS), "first difference method" (NOAA). I mention these just to say that it is a real problem that major efforts have been made to overcome.
As a quick and mostly OK fix, I recommend using regression fits for a common year, as described here. But the more complete method is a combined regression as used in TempLS (details here)
Update - to be more specific, as in the link it is best to do this in conjunction with some scheme for preferring data local to a region. There I used weighting. But to stick closest to the convention of using a fixed interval like 1961-90, my process would be:
1. If there is enough data in that interval (say 80%) use the regression mean over the interval
2. If not, then extend the interval to the minimum extent necessary to get 30 (or 24) years of data.
The anomaly fix
So I've done a combined regression average:

It's clearly warming since about 1940. And by about a degree.
Other evidence of warming
The station trends over their observed periods are almost all positive. So they are over a fixed period. Here, from the active trend map is a snap of trends in Australia since 1967:

Plots of the station data are somewhat obscured by noise. From Climate Etc:
It is rising. But a modest degree of smoothing - a 9 point triangular filter, gives:

The uptrend is now unmistakeable.
Tuesday, March 17, 2015
February GISS up 0.04°C
late news, but I've already posted twice on February temp. This is the regular post comparing GISS with TempLS.
GISS rose from 0.75°C in Jan to 0.79°C as predicted by Olof and JCH. TempLS also rose by a small amount. Troposphere measures showed a small decline.
Here is the GISS map. As with TempLS, very strong features - Russia and N Europe warm, East N America cold, and the West warm. Also a warm spot in Sudan - I had thought it might be a TempLS artefact.

And here is the corresponding TempLS map, as on St Patrick's Day:

GISS rose from 0.75°C in Jan to 0.79°C as predicted by Olof and JCH. TempLS also rose by a small amount. Troposphere measures showed a small decline.
Here is the GISS map. As with TempLS, very strong features - Russia and N Europe warm, East N America cold, and the West warm. Also a warm spot in Sudan - I had thought it might be a TempLS artefact.

And here is the corresponding TempLS map, as on St Patrick's Day:

Friday, March 13, 2015
February TempLS was warm
China GHCN data was late, but is now in (report here). The global average temperature was 0.694°C, slightly up from Jan 0.674. A small rise, but January had already tied May 2014, which was the hottest month of last year. So it's a warm start to 2015. The last month warmer than Feb was Nov 2013.
The map is pretty simple. A big warm band across Russia and NE Europe. Cold in E N America, but warm in the W and Akaska.
The map is pretty simple. A big warm band across Russia and NE Europe. Cold in E N America, but warm in the W and Akaska.
Tuesday, March 10, 2015
Derivatives and regression again
I've been writing about how a "sliding" trend may function as a estimate of derivative (and what might be better) here, here, here and here. There has been discussion, particularly commenter Greg. This post just catches up on some things that arose.

These are scaled to give correct derivative for a line. On the legend, I have written beside each the RMS value. Sqrt of the integral of square. That's the factor that you would expect to multiply white noise, as a variance of weighted sum. Ordinary regression has the least value. That is an aspect of its optimal quality. Better smoothing for HF comes at a cost.
So now to apply these to a sinusoid. In the following plot the yellow is the sine to be differentiated, the continuous curve "Deriv" is the exact derivative, and I have applied the three windows with three different footprints (line types). At each end, a region equal to half a footprint is lost - I have marked those parts with a horizontal line, which tells you how long each footprint was.

The first thing to note is that each gives a sinusoid, with the correct 90° phase shift. The is a consequence of being an odd function. Second is that as the footprint broadens, the amplitude shrinks. The inaccuracy is because a wider footprint is more affected by higher derivatives of the sine. In effect, it smoothes the result, to no good purpose here. But when there is noise, the smoothing is needed. That is the basic trade-off that we will encounter.
You'll notice, too, that both the Welch and step do better than regression. This is basically because they are weighted to favor central values, rather than any more subtle merit.
Now for something different, to differentiate white noise. There should be no real trend. I've dropped the step filter. Again the horizontal end sections indicate the half-footprint.

Now what shows is a marked oscillation, with period about equal to the footprint. The Welch filter is good at damping frequencies beyond this range; however, the actual amplitude of the response is much higher. That is associated with the higher RMS value noted on the first figure, and is commensurate with it.

The pale grey is the original, sine and total. The blue is the derivative of sine. The red OLS regression tracks better than the smoother purple, but has more residual HF. Again the half-footprint is shown by the level sections at each end.
A way to do this is to take a family of windows, and make them orthogonal to higher powers by Gram-Schmidt orthogonalisation. I did that using OLS, OLS with Welch taper, and OLS with Welch^2 (W0,W1,W0). Here are the resulting windows. W1 is guaranteed to be accurate for a cubic, and W2 for fifth order:

Again, they are scaled to give the same derivative. We see a more extreme version of the RMS inflation of the first fig. The higher order accuracy is got at a cost of much larger coefficients. They do indeed differentiate better, as the next plot shows:

W2 seems suspiciously perfect. But each result is just the correct sinusoid multiplied by a scalar, and I think it just approaches 1 in an oscillatory way, so W2 just happens to be a zero. Anyway, here higher order certainly works. What about with white noise?

Here is the downside. The higher orders amplify noise, in line with their RMS integrals.
Higher order may sometimes work. If you have an exact cubic, then you can expand the footprint as far as data permits without loss of derivative accuracy, and thus maybe overcome the RMS loss. But generally not.
Does it differentiate?
Greg is not so sure. I'll give some examples. First here is a graph of some of the windows. I've added a step function, to show that in fact virtually any odd function will differentiate. The one called Welch^2 is the linear window multiplied by the square of a Welch taper. There is information about the Welch taper, and why it arises naturally here, here.
These are scaled to give correct derivative for a line. On the legend, I have written beside each the RMS value. Sqrt of the integral of square. That's the factor that you would expect to multiply white noise, as a variance of weighted sum. Ordinary regression has the least value. That is an aspect of its optimal quality. Better smoothing for HF comes at a cost.
So now to apply these to a sinusoid. In the following plot the yellow is the sine to be differentiated, the continuous curve "Deriv" is the exact derivative, and I have applied the three windows with three different footprints (line types). At each end, a region equal to half a footprint is lost - I have marked those parts with a horizontal line, which tells you how long each footprint was.

The first thing to note is that each gives a sinusoid, with the correct 90° phase shift. The is a consequence of being an odd function. Second is that as the footprint broadens, the amplitude shrinks. The inaccuracy is because a wider footprint is more affected by higher derivatives of the sine. In effect, it smoothes the result, to no good purpose here. But when there is noise, the smoothing is needed. That is the basic trade-off that we will encounter.
You'll notice, too, that both the Welch and step do better than regression. This is basically because they are weighted to favor central values, rather than any more subtle merit.
Now for something different, to differentiate white noise. There should be no real trend. I've dropped the step filter. Again the horizontal end sections indicate the half-footprint.

Now what shows is a marked oscillation, with period about equal to the footprint. The Welch filter is good at damping frequencies beyond this range; however, the actual amplitude of the response is much higher. That is associated with the higher RMS value noted on the first figure, and is commensurate with it.
Integrating with noise
OK, so what happens if we estimate the derivative of a sinusoid with noise. The next fig has sine with gaussian noise of equal amplitude added. Can we recover the derivative?
The pale grey is the original, sine and total. The blue is the derivative of sine. The red OLS regression tracks better than the smoother purple, but has more residual HF. Again the half-footprint is shown by the level sections at each end.
Improving the derivative formula
Pekka, on another thread, recommended taking pairs of points, differencing, and forming some kind of optimal derivative as a weighted sum. Odd function windows automatically give such a weighted sum. The idea of improving the derivative (higher order) is attractive, because it allows the footprint to be expanded, with better noise damping, without loss of derivative accuracy.A way to do this is to take a family of windows, and make them orthogonal to higher powers by Gram-Schmidt orthogonalisation. I did that using OLS, OLS with Welch taper, and OLS with Welch^2 (W0,W1,W0). Here are the resulting windows. W1 is guaranteed to be accurate for a cubic, and W2 for fifth order:

Again, they are scaled to give the same derivative. We see a more extreme version of the RMS inflation of the first fig. The higher order accuracy is got at a cost of much larger coefficients. They do indeed differentiate better, as the next plot shows:

W2 seems suspiciously perfect. But each result is just the correct sinusoid multiplied by a scalar, and I think it just approaches 1 in an oscillatory way, so W2 just happens to be a zero. Anyway, here higher order certainly works. What about with white noise?

Here is the downside. The higher orders amplify noise, in line with their RMS integrals.
Higher order may sometimes work. If you have an exact cubic, then you can expand the footprint as far as data permits without loss of derivative accuracy, and thus maybe overcome the RMS loss. But generally not.
Thursday, March 5, 2015
Klotzbach revisited
Not a perfect title; it's actually my first comment on the 2009 GRL paper by Klotzbach, Pielke's, Christy et al. It was controversial at the time, but that was pre-Moyhu, or at least in very early days. And I hadn't paid it much attention. But it surfaced again today at Climate Etc, so I thought I should read it.
The paper is very lightweight (as contrarian papers can be). It argues that observed surface trends since 1979 actually exceed troposphere trends, as measured by the UAH and RSS indices, which CMIP etc modelling suggests that the troposphere should warm faster.
Now for global you can simply get those trends, and many more, with CIs from the Moyhu trend viewer. You might say, well, figuring out what the models said should be rated substantial. But they way oversimplified, were corrected at Real Climate (Gavin) and had to publish a corrigendum. There has been more discussion then and over the years. Here, for example, is a post at Climate Audit, with Gavin participating. But the audit didn't seem to pick up the CI issue, though other methods were discussed. Later a Klotzbach revisited WUWT post (my title echoes) two years ago; more on that from SKS here. And now another update.
But what no-one, AFAICS, has noticed is that the claims of statistical significance are just nuts. And significance is essential, because they have only one observation period. The claim originally, from the abstract, was:
Update: I think that the CI's they are quoting may relate to a different calculation. They computed the trends in Table 1, with CI's, and in Table 2 the differences. They say in the abstract that these are differences of trends, but the heading of Table 2, which is not very clear, could mean that they are computing the trends of the differences (a new regression) and giving CI's for that. That is actually a reasonable thing to do, but they should make it clear. I have got reasonably close to their numbers for comparisons with UAH, but not with RSS; it may be that the RSS data has changed significantly since 2009.
I'll describe this in more detail below the jump.
Here is their Table 1 of trends in C/decade with 95% CI's
My own calcs (to 2014) gave CI's comparable to these.
I've been commenting at CE here and here, and I extracted σ values here
But you don't need them to see that the results in Table 1 are very unlikely to be significant. Virtually all the trends lie within the CIs of the sat indices. Consider a comparison of NCDC 0.16 and UAH 0.13 [0.06-0.19]. There is no way NCDC is inconsistent with the range of UAH, even if it did not have error of its own.
Anyway, what Klotzbach et al did was to show a table of differences with CIs:
So compare, say, Had-UAH global: 0.03 [0.00- 0.07]
But Had was:
Hadley Surface 0.16 [0.12-0.21]
and UAH
UAH Lower Trop 0.13 [0.06-0.19] 0.06
The CI for the difference has about half the range as for RSS alone. This is reflected throughout the table. But the normal method requires that σ's be added in quadrature. The range for the difference must be larger than for each of the operands.
Now it might be possible to construct an argument that dependence would make a lower CI for the difference. But there isn't much data to resolve dependence as well. And this is basically a test for dependence. You can't start off by assuming it. In any case, the paper doesn't say anything about how the difference CI's were calculated. And I have no idea.
Table 3 shows the differences between amplified (x 1.2) surface vs troposphere. It is little different, and again the CI's are far too narrow. Yet that is where the main claim of significance is based. I won't reproduce here; it is muddied by the changes made in the corrigendum. But they do nothing to repair the situation.
I do not believe any of these trend differences are significant.
Update - see above. I think that interpreted as the CI's of a regression on the differences, the original significance claims may be justified.
Update. A commenter at Climate Etc challenged me to calculate a corrected Table 2. He also wanted Table 3, but it's a bit late for that. Here is Table 2. I've shown under each original line, my variance-added numbers. I've worked with rounded data, so there are rounding discrepancies.
The paper is very lightweight (as contrarian papers can be). It argues that observed surface trends since 1979 actually exceed troposphere trends, as measured by the UAH and RSS indices, which CMIP etc modelling suggests that the troposphere should warm faster.
Now for global you can simply get those trends, and many more, with CIs from the Moyhu trend viewer. You might say, well, figuring out what the models said should be rated substantial. But they way oversimplified, were corrected at Real Climate (Gavin) and had to publish a corrigendum. There has been more discussion then and over the years. Here, for example, is a post at Climate Audit, with Gavin participating. But the audit didn't seem to pick up the CI issue, though other methods were discussed. Later a Klotzbach revisited WUWT post (my title echoes) two years ago; more on that from SKS here. And now another update.
But what no-one, AFAICS, has noticed is that the claims of statistical significance are just nuts. And significance is essential, because they have only one observation period. The claim originally, from the abstract, was:
"The differences between trends observed in the surface and lower-tropospheric satellite data sets are statistically significant in most comparisons, with much greater differences over land areas than over ocean areas."I've noticed that the authors are quieter on this recently, and it may be that someone has noticed. But without statistical significance, the claims are meaningless.
Update: I think that the CI's they are quoting may relate to a different calculation. They computed the trends in Table 1, with CI's, and in Table 2 the differences. They say in the abstract that these are differences of trends, but the heading of Table 2, which is not very clear, could mean that they are computing the trends of the differences (a new regression) and giving CI's for that. That is actually a reasonable thing to do, but they should make it clear. I have got reasonably close to their numbers for comparisons with UAH, but not with RSS; it may be that the RSS data has changed significantly since 2009.
I'll describe this in more detail below the jump.
Here is their Table 1 of trends in C/decade with 95% CI's
Table 1. Global, Land, and Ocean Per Decade Temperature Trends and Ratios Over the Period From 1979 to 2008 Data Set Global Tren Land Ocean Trend NCDC Surface 0.16 [0.12-0.20] 0.31 [0.23-0.39] 0.11 [0.07-0.15] Hadley Surface 0.16 [0.12-0.21] 0.22 [0.17-0.28] 0.14 [0.08-0.19] UAH Lower Trop 0.13 [0.06-0.19] 0.16 [0.08-0.25] 0.11 [0.04-0.17] RSS Lower Trop 0.17 [0.10-0.23] 0.20 [0.12-0.29] 0.13 [0.08-0.19]
My own calcs (to 2014) gave CI's comparable to these.
I've been commenting at CE here and here, and I extracted σ values here
NCDC Surface 0.16 [0.12-0.20] 0.04 Hadley Surface 0.16 [0.12-0.21] 0.04 UAH Lower Trop 0.13 [0.06-0.19] 0.06 RSS Lower Trop 0.17 [0.10-0.23] 0.06
But you don't need them to see that the results in Table 1 are very unlikely to be significant. Virtually all the trends lie within the CIs of the sat indices. Consider a comparison of NCDC 0.16 and UAH 0.13 [0.06-0.19]. There is no way NCDC is inconsistent with the range of UAH, even if it did not have error of its own.
Anyway, what Klotzbach et al did was to show a table of differences with CIs:
Table 2. Global, Land, and Ocean Per Decade Temperature Trends Over the Period From 1979 to 2008 for the NCDC Surface Analysis Minus UAH Lower Troposphere Analysis and the Hadley Centre Surface Analysis Minus RSS Lower Troposphere Analysis Data Set Global Trend (C) Land Trend (C) Ocean Trend (C) NCDC minus UAH 0.04 [0.00- 0.08] 0.15 [0.08- 0.21] 0.00 [-0.04-0.05] NCDC minus RSS 0.00 [-0.04- 0.04] 0.11 [0.07- 0.15] -0.02 [-0.07- 0.02] Hadley Center minus UAH 0.03 [0.00- 0.07] 0.06 [0.02- 0.10] 0.03 [-0.01-0.07] Hadley Center minus RSS -0.01 [-0.04- 0.03] 0.02 [-0.02- 0.06] 0.00 [-0.04-0.04] Trends that are statistically significant at the 95% level are bold; 95% confidence intervals are given in brackets.
So compare, say, Had-UAH global: 0.03 [0.00- 0.07]
But Had was:
Hadley Surface 0.16 [0.12-0.21]
and UAH
UAH Lower Trop 0.13 [0.06-0.19] 0.06
The CI for the difference has about half the range as for RSS alone. This is reflected throughout the table. But the normal method requires that σ's be added in quadrature. The range for the difference must be larger than for each of the operands.
Now it might be possible to construct an argument that dependence would make a lower CI for the difference. But there isn't much data to resolve dependence as well. And this is basically a test for dependence. You can't start off by assuming it. In any case, the paper doesn't say anything about how the difference CI's were calculated. And I have no idea.
Table 3 shows the differences between amplified (x 1.2) surface vs troposphere. It is little different, and again the CI's are far too narrow. Yet that is where the main claim of significance is based. I won't reproduce here; it is muddied by the changes made in the corrigendum. But they do nothing to repair the situation.
I do not believe any of these trend differences are significant.
Update - see above. I think that interpreted as the CI's of a regression on the differences, the original significance claims may be justified.
Update. A commenter at Climate Etc challenged me to calculate a corrected Table 2. He also wanted Table 3, but it's a bit late for that. Here is Table 2. I've shown under each original line, my variance-added numbers. I've worked with rounded data, so there are rounding discrepancies.
Data Set Global Trend (C) Land Trend (C) Ocean Trend (C)
NCDC minus UAH 0.04 [0.00- 0.08] 0.15 [0.08- 0.21] 0.00 [-0.04-0.05]
0.03 -0.05 0.11 0.15 0.03 0.27 0.00 -0.08 0.08
NCDC minus RSS 0.00 [-0.04- 0.04] 0.11 [0.07- 0.15] -0.02 [-0.07- 0.02]
-0.01 -0.09 0.07 0.11 -0.01 0.23 -0.02 -0.09 0.05
Hadley Center minus UAH 0.03 [0.00- 0.07] 0.06 [0.02- 0.10] 0.03 [-0.01-0.07]
0.03 -0.05 0.11 0.06 -0.04 0.16 0.03 -0.06 0.12
Hadley Center minus RSS -0.01 [-0.04- 0.03] 0.02 [-0.02- 0.06] 0.00 [-0.04-0.04]
-0.01 -0.09 0.07 0.02 -0.08 0.12 0.01 -0.07 0.09
As you can see, there is now only one case that is barely significant - NCDC-UAH on land. But that is at 95% - we could expect it 1 in 20 times. And here are 12 tests.
Tuesday, March 3, 2015
Early comment on global February
According to my NCEP/NCAR based index, February was globally pretty warm. Very warm indeed around the 12th, but a cool start and finish. The hotspot was Central Asia/Mongolia (daily eyeballing estimate). It ended up just a little cooler than October, which after May was warmest in 2014.
I'll have a TempLS surface report in a few days.
Update. Preliminary TempLS (7 mar) is very warm indeed. In fact, warmest month ever (since 1900). But Canada, Australia, China, India still to come. Very warm in Russia and N and E Europe. Cold in E US/Can.
Update 8 Mar. Canada, Australia, India are in. Canada was cold. TempLS has come back to 0.7, below warmest ever (March 2010 at 0.737°C). Still, since 2010 only Nov 2013 has been warmer, and only slightly. There is a little more data to come.
I'll have a TempLS surface report in a few days.
Update. Preliminary TempLS (7 mar) is very warm indeed. In fact, warmest month ever (since 1900). But Canada, Australia, China, India still to come. Very warm in Russia and N and E Europe. Cold in E US/Can.
Update 8 Mar. Canada, Australia, India are in. Canada was cold. TempLS has come back to 0.7, below warmest ever (March 2010 at 0.737°C). Still, since 2010 only Nov 2013 has been warmer, and only slightly. There is a little more data to come.
Monday, March 2, 2015
Derivatives, filters, odds and ends
I've been writing about how a "sliding" trend may function as a estimate of derivative (and what might be better) here, here and here. There has been discussion, particularly commenter Greg. This post just catches up on some things that arose.
(π²/3)*(w/2)^(.5-n)*Γ(n+1.5)*Jn+.5(x)
where x=f*π*T, f=freq in 1/Cen, T=trend period,n=1,2,3...
I've given a detailed derivation here. You might think that Bessel functions is overkill. But in fact, j0(x)= sqrt(π/2x)J1/2(x) is just the sinc function sin(x)/x, and as jn increase in order, they are just trig functions multiplied by polynomials in 1/x, in such a was that they are O(xn) near 0, and decay as 1/x for large x. So x1-njn has the appropriate asymptotics here, and for the order of the polynomials, uniquely so.
Properties that you are likely to want in a lowish pass convolution filter are:
The ideal filter with compact support and bounded domain is that gate or boxcar filter H(t). But in the frequency domain is a sinc function sin(ω)/ω, which attenuates very slowly. There is a rule about rates of attenuation. The power |ω|-n of attenuation is determined by n, the order of the first derivative that fails to exist. This is usually determined by the cut-off at the ends of the compact support of the filter. H(t) is discontinuous, to the first derivative fails.
There are filters, like Welch, or the triangle filters (see Wiki for a list) which terminate with a discontinuous derivative. These attenuate O(|ω|-2). It is fairly easy to extend to a zero derivative at the end, as with Hann, Blackman, and so increase n to 3 or beyond. These satisfy 1 and 2. For Welch W, raising it to the nth power improves the termination by a power of n, and the corresponding HF attenuation.
The ultimate in this direction is the Gaussian. It gives best roll-off in the freq domain (FD). It does not strictly have bounded support, but approaches zero so fast that it can be truncated, with only a small amplitude HF tail (though slowly fading). This can be ameliorated. But again, it does not have a flat top.
The Lanczos window tries more to honor requirement 3 by reintroducing aspects of the sinc function in the time domain. It is a product of a narrow and a wider sinc, generally arranged so that the zeroes coincide at the cut-off. It gives a flatter top in the FD, at the cost of being non-positive in the TD.
I find that Welch functions are flexible. You can raise them to any power to give faster attenuation, at the expense of a broader footprint in the FD relative to the support in the TD (so attenuation is eventually faster, but starts later).
So here are the plots of the windows. I've normalised to area=1, except for Lanczos, shown with area=0.5 (for the sake of the y-axis). But it is restored for the spectrum.

W stands for Welch. You can see that the higher powers are looking quite like the Gaussian. So here are the spectra:

You can see the trade-offs. W decays relatively slowly, but is narrowest in the FD - for its TD footprint, it has a narrower low-pass. Higher powers approach the Gaussian. The Lanczos does indeed have a flatter top, as intended, and also a good attenuation. But it is broadest of all - it lets through relatively high frequencies before the cut-off.
Welch smoothing and spherical Bessel functions.
In the first post, I gave this plot of the spectra of the 10-year OLS trend operator, and what results if multiplied by a Welch taper W, and then multiply again. I'll explain why those operations below. T the spectra are actually spherical Bessel functions. Or, more exactly,(π²/3)*(w/2)^(.5-n)*Γ(n+1.5)*Jn+.5(x)
where x=f*π*T, f=freq in 1/Cen, T=trend period,n=1,2,3...
I've given a detailed derivation here. You might think that Bessel functions is overkill. But in fact, j0(x)= sqrt(π/2x)J1/2(x) is just the sinc function sin(x)/x, and as jn increase in order, they are just trig functions multiplied by polynomials in 1/x, in such a was that they are O(xn) near 0, and decay as 1/x for large x. So x1-njn has the appropriate asymptotics here, and for the order of the polynomials, uniquely so.
General remarks on filters
Greg has been commenting on the merits of other filters, including Gaussian and Lanczos. They are of course not strictly differentiating filters, but could be converted to one. In fact, any of the usual symmetric windows/filters can be converted by differentiating to a differentiating filter (the reason is not quite as obvious as it sounds).Properties that you are likely to want in a lowish pass convolution filter are:
- In the time domain, a bounded domain (compact support). In fact, the domain should about match the period corresponding to the upper limit of frequencies that you want to start attenuating.
- In the frequency domain, eventual rapid attenuation with high frequency, which often means controlling side lobes
- Sometimes overlooked, a contrary wish for some specific behaviour in the pass band. Possibly a flat response for low pass, or in our case, an accurate derivative representation.
The ideal filter with compact support and bounded domain is that gate or boxcar filter H(t). But in the frequency domain is a sinc function sin(ω)/ω, which attenuates very slowly. There is a rule about rates of attenuation. The power |ω|-n of attenuation is determined by n, the order of the first derivative that fails to exist. This is usually determined by the cut-off at the ends of the compact support of the filter. H(t) is discontinuous, to the first derivative fails.
There are filters, like Welch, or the triangle filters (see Wiki for a list) which terminate with a discontinuous derivative. These attenuate O(|ω|-2). It is fairly easy to extend to a zero derivative at the end, as with Hann, Blackman, and so increase n to 3 or beyond. These satisfy 1 and 2. For Welch W, raising it to the nth power improves the termination by a power of n, and the corresponding HF attenuation.
The ultimate in this direction is the Gaussian. It gives best roll-off in the freq domain (FD). It does not strictly have bounded support, but approaches zero so fast that it can be truncated, with only a small amplitude HF tail (though slowly fading). This can be ameliorated. But again, it does not have a flat top.
The Lanczos window tries more to honor requirement 3 by reintroducing aspects of the sinc function in the time domain. It is a product of a narrow and a wider sinc, generally arranged so that the zeroes coincide at the cut-off. It gives a flatter top in the FD, at the cost of being non-positive in the TD.
I find that Welch functions are flexible. You can raise them to any power to give faster attenuation, at the expense of a broader footprint in the FD relative to the support in the TD (so attenuation is eventually faster, but starts later).
Plots
That was all a longish preamble to fulfilling a request from Greg to plot spectra of the Gaussian (truncated at 3 σ), and Lanczos, along with the Welch functions I have been using.So here are the plots of the windows. I've normalised to area=1, except for Lanczos, shown with area=0.5 (for the sake of the y-axis). But it is restored for the spectrum.

W stands for Welch. You can see that the higher powers are looking quite like the Gaussian. So here are the spectra:

You can see the trade-offs. W decays relatively slowly, but is narrowest in the FD - for its TD footprint, it has a narrower low-pass. Higher powers approach the Gaussian. The Lanczos does indeed have a flatter top, as intended, and also a good attenuation. But it is broadest of all - it lets through relatively high frequencies before the cut-off.