<h2>Seasonal insolation</h2>

This post was started by some recent posting at WUWT. It's about the expected thermal effect of the Earth's eccentric orbit. It produces a variable total solar insolation for the planet, which one might expect to be reflected in temperatures. A few days ago, Willis contrasted the small solar cycle fluctuation which this much larger oscillation, suggesting that if we couldn't detect the orbital effect then the solar cycle couldn't be much. And just now, Stan Robertson at WUWT took up the idea, looking for the eccentricity in annual global anomaly indices.

I've also wondered the effect of eccentricity. But when you think about anomalies, it is clear that they subtract out any annual cycle. So the effect can't be found there. And in fact it's going to be hard to disentangle it from axis tilt effect. A GCM could of course run alternatively with a circular orbit, which would determine it.

Anyway, someone posted a plot of average daily insolation against time of year and latitude. That is, at TOA, or for an airless Earth. I was surprised that the maximum for the year was at the solstice at the relevant Pole. I found a good plot and the relevant maths in Wikipedia. So I'll show that below the jump, with a brief version of the math, and a plot of variation with latitude at the solstice. It isn't even monotonic.

So here is the plot, with caption also from Wiki.



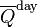, the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S₀ = 1367 W m⁻², obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m⁻².

y axis is latitude, x axis is angle of orbit, starting at the March equinox. You can see the effect of orbit eccentricity in making the S pole warmer. That pole also shows clearly the non-monoticity; there is a pinch near the Antarctic circle.

So here is the Wiki math, using the above notation:
Solve

for h_o
Solve

for δ
But here I find a vary rare math error in Wiki. The last term should not have an ω. So I removed it.

Now substituting

in

we have the solution.

I used this to plot the solstice curves:



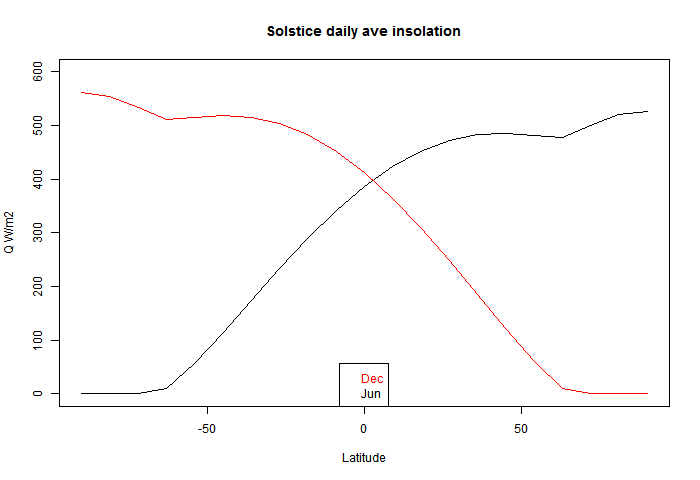
You can see that there is a discontinuity of (2nd - see PP in comments) derivative at the polar circles, where one goes into night, and the other gets the benefit of 24 hr insolation, which is enough to exceed even average daily tropical insolation (of course, without atmospheric losses).